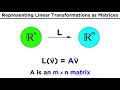
Linear Transformations and Their Properties
Interactive Video
•
Mathematics
•
9th - 12th Grade
•
Hard
Thomas White
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the primary function of a linear transformation in vector spaces?
To map vectors from one space to another
To add vectors
To multiply vectors
To divide vectors
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which of the following is a possible outcome of a linear transformation?
A vector of the same length
A matrix of different dimensions
A scalar
All of the above
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What must be true for a transformation to be considered linear?
It must only map within the same vector space
It must satisfy scalar multiplication and vector addition properties
It must map vectors to scalars
It must preserve vector length
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the example mapping L: R2 → R3, what is the result of transforming the vector (1, 0)?
(0, 0, 1)
(1, 0, 0)
(0, 1, 1)
(1, 1, 0)
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How can the commutativity of operations in linear transformations be described?
Only scalar multiplication is commutative
Operations must be performed in a specific order
Only vector addition is commutative
The order of operations does not affect the result
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is a key benefit of representing linear transformations as matrices?
It simplifies the transformation process
It allows for non-linear transformations
It restricts transformations to R2
It eliminates the need for vector spaces
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of transforming the standard basis vector (0, 1) in the example mapping?
(1, 0, 0)
(0, 1, 1)
(0, 0, 1)
(1, 1, -1)
Create a free account and access millions of resources
Create resources
Host any resource
Get auto-graded reports

Continue with Google

Continue with Email

Continue with Classlink

Continue with Clever
or continue with

Microsoft
%20(1).png)
Apple
Others
By signing up, you agree to our Terms of Service & Privacy Policy
Already have an account?
Similar Resources on Wayground

6 questions
Solving Systems and Absolute Value
Interactive video
•
9th - 12th Grade

11 questions
Exploring Compound Interest Concepts
Interactive video
•
9th - 12th Grade

8 questions
REFUTACIÓN COMPLETA del #RetoMateMagia! Te demuestro que 1≠ 0 (de 6 formas diferentes)
Interactive video
•
9th - 10th Grade

8 questions
Solving an equation using the half angle formula of sine
Interactive video
•
11th Grade - University

8 questions
Graphing logarithmic equations
Interactive video
•
11th Grade - University
Popular Resources on Wayground

20 questions
Halloween Trivia
Quiz
•
6th - 8th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

15 questions
Order of Operations
Quiz
•
5th Grade

20 questions
Halloween
Quiz
•
5th Grade

16 questions
Halloween
Quiz
•
3rd Grade

12 questions
It's The Great Pumpkin Charlie Brown
Quiz
•
1st - 5th Grade

20 questions
Possessive Nouns
Quiz
•
5th Grade

10 questions
Halloween Traditions and Origins
Interactive video
•
5th - 10th Grade
Discover more resources for Mathematics

10 questions
Halloween Trivia Challenge
Interactive video
•
6th - 10th Grade

15 questions
Halloween Trivia
Quiz
•
9th Grade

20 questions
Translations, Reflections & Rotations
Quiz
•
8th - 10th Grade

19 questions
Halloween Fun
Quiz
•
6th - 10th Grade

15 questions
Two Step Equations
Quiz
•
9th Grade

20 questions
Parallel and Perpendicular lines
Quiz
•
9th Grade

10 questions
Types of Slope
Quiz
•
6th - 9th Grade

20 questions
Slope from Two Points
Quiz
•
9th Grade