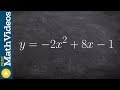
Perfect Square Trinomials and Quadratics

The video tutorial explains the process of identifying and forming perfect square trinomials. It begins with an introduction to perfect square trinomials and the initial problem setup. The teacher then discusses factoring and grouping terms to form a perfect square. The process of completing the square is detailed, including dividing the middle term by two and squaring it. The tutorial emphasizes ensuring equation equality and making necessary adjustments. Finally, the video concludes with finalizing the perfect square trinomial and summarizing the key points.

What is a perfect square trinomial?

• A trinomial with no square terms.

• A trinomial with all positive coefficients.

• A trinomial that can be factored into a binomial squared.

• A trinomial that cannot be factored.

What is the first step in identifying a perfect square trinomial?

• Check if the first term is a square term.

• Add a constant to the equation.

• Subtract the middle term.

• Multiply all terms by 2.

Why is the given example not a perfect square trinomial?

• It has a negative coefficient.

• It lacks a square term.

• It is already factored.

• It has an extra term.

What is the first step in grouping terms?

• Multiply all terms by 2.

• Add a constant term.

• Factor out the greatest common factor.

• Identify the square term.

Why is it important to have a square term as the first term?

• It simplifies the equation.

• It ensures the trinomial can be factored.

• It eliminates the need for constants.

• It makes the equation linear.

What does factoring out a negative number help achieve?

• It changes the sign of the equation.

• It eliminates the need for further factoring.

• It simplifies the equation.

• It sets up the equation for completing the square.

How do you complete the square?

• Add the square of the middle term.

• Multiply the middle term by 2.

• Subtract the square of the middle term.

• Divide the middle term by 2 and square it.

What happens if the middle term is not divisible by 2?

• The equation is linear.

• The equation is already a perfect square.

• The equation cannot be factored.

• The equation needs to be adjusted.

What is the role of the constant term in a perfect square trinomial?

• It completes the square.

• It changes the vertex.

• It has no role.

• It determines the direction of the graph.

Why is it important to consider multiplication factors when comparing equations?

• To simplify the equations.

• To avoid errors in calculation.

• To make the equations identical.

• To ensure the equations are balanced.