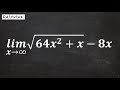
Limits and Infinity Concepts
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Practice Problem
•
Hard
Thomas White
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the primary focus when discussing limits at infinity?
Analyzing the behavior of functions as x approaches infinity
Understanding the behavior of functions as x approaches zero
Calculating the derivative of functions at infinity
Determining the exact value of infinity
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
When x approaches infinity, what happens to the square root of infinity?
It becomes infinity
It remains finite
It becomes zero
It becomes negative
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of adding infinity to infinity?
A finite number
Zero
Infinity
Negative infinity
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the main issue when subtracting infinity from infinity?
The result is always negative
The result is always zero
It is indeterminate which infinity is larger
The result is always infinity
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is an indeterminate form?
A form where the result is always infinity
A form where the result cannot be determined
A form where the result is always zero
A form where the result is always negative
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why is rationalization important in solving limits?
To make the expression negative
To increase the power of x
To simplify the expression and remove indeterminacy
To make the expression more complex
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the purpose of using a conjugate in rationalization?
To eliminate square roots and simplify the expression
To change the sign of the expression
To add more terms to the expression
To make the expression infinite
Access all questions and much more by creating a free account
Create resources
Host any resource
Get auto-graded reports
Continue with Google
Continue with Email
Continue with Microsoft
or continue with
%20(1).png)
Apple
Others
By signing up, you agree to our Terms of Service & Privacy Policy
Already have an account?
