What is the initial problem presented in the video?
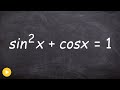
Trigonometric Identities and Equations
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Hard
Thomas White
FREE Resource
Read more
9 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Tangent squared of x plus sine of x
Cosine squared of x plus sine of x
Sine of x plus cosine squared of x
Sine squared of x plus cosine of x
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why can't the expression be factored initially?
The expression is a simple addition
The expression is already factored
Sine and cosine have common terms
Sine and cosine do not have common terms
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What identity is used to simplify the expression?
Sum of angles identity
Double angle identity
Pythagorean identity
Reciprocal identity
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of substituting using the Pythagorean identity?
Sine squared of x equals 1 plus cosine squared of x
Sine squared of x equals cosine squared of x
Cosine squared of x equals 1 minus sine squared of x
Sine squared of x equals 1 minus cosine squared of x
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the purpose of factoring out negative one?
To simplify the equation
To eliminate the cosine term
To make the equation more complex
To change the equation to a different form
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the next step after setting the equation to zero?
Solve for y
Apply the quadratic formula
Factor the equation
Use the sine identity
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
When does cosine of x equal zero on the unit circle?
At π/2 and 3π/2
At 0 and 2π
At 0 and π
At π and 2π
8.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the general solution for when cosine of x equals one?
θ = 0 + 2πr
θ = 3π/2 + πr
θ = π/2 + πr
θ = π + 2πr
9.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the general solution for when cosine of x equals zero?
θ = 3π/2 + πr
θ = 0 + 2πr
θ = π/2 + πr
θ = π + 2πr
Similar Resources on Quizizz

11 questions
Trigonometric Functions and Their Properties
Interactive video
•
9th - 10th Grade

11 questions
Trigonometric Functions and Identities
Interactive video
•
9th - 10th Grade

11 questions
Periodic Properties of Trigonometric Functions
Interactive video
•
9th - 10th Grade

11 questions
Trigonometric Functions and Derivatives
Interactive video
•
9th - 10th Grade

6 questions
Verify an identity with double angle identities
Interactive video
•
9th - 10th Grade

6 questions
Simplify a trig expression by multiplying by the LCD
Interactive video
•
9th - 10th Grade

6 questions
Understanding the relationship of polar and rectangular coordinates
Interactive video
•
9th - 10th Grade

9 questions
Trigonometric Functions and Identities
Interactive video
•
9th - 10th Grade
Popular Resources on Quizizz

15 questions
Multiplication Facts
Quiz
•
4th Grade

20 questions
Math Review - Grade 6
Quiz
•
6th Grade

20 questions
math review
Quiz
•
4th Grade

5 questions
capitalization in sentences
Quiz
•
5th - 8th Grade

10 questions
Juneteenth History and Significance
Interactive video
•
5th - 8th Grade

15 questions
Adding and Subtracting Fractions
Quiz
•
5th Grade

10 questions
R2H Day One Internship Expectation Review Guidelines
Quiz
•
Professional Development

12 questions
Dividing Fractions
Quiz
•
6th Grade