Understanding Similar Triangles Concepts

This video tutorial explains how to solve problems involving similar triangles. It begins with identifying similar triangles using parallel lines and angles, then moves on to finding scalar factors and setting up proportions. The tutorial demonstrates solving for unknown sides X and Y using these methods. It includes a real-world example involving a lamp post and a person to illustrate the application of similar triangles. The video concludes with another example using parallel lines and similar triangles, emphasizing the importance of understanding proportions and scalar factors.

What is the first step in solving problems involving similar triangles?

• Determine the type of triangles

• Find the perimeter of the triangles

• Calculate the area of the triangles

• Identify the parallel lines

Which angle relationship is used to prove triangles are similar?

• Supplementary angles

• Corresponding angles

• Complementary angles

• Alternate interior angles

What is a scalar factor in the context of similar triangles?

• A measure of the triangle's area

• A ratio of corresponding side lengths

• The sum of all angles in a triangle

• The difference between the longest and shortest sides

How do you find the length of an unknown side in similar triangles?

• By using the Pythagorean theorem

• By setting up a proportion with the scalar factor

• By measuring directly

• By calculating the area first

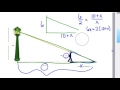
In the lamp post example, what is the height of the lamp post?

• 6 meters

• 5 meters

• 4 meters

• 7 meters

What is the length of the shadow in the lamp post example?

• 6 meters

• 5 meters

• 4 meters

• 3 meters

In the parallel lines example, what is the length of side EC?

• 3.5

• 2.5

• 1.5

• 4.5

What is the importance of drawing triangles separately in the examples?

• To make them look bigger

• To measure them accurately

• To change their orientation

• To avoid confusion and set up proportions easily

Why is cross-multiplying not always recommended?

• It is too complicated

• It can lead to errors if overused

• It is not applicable to all problems

• It requires a calculator