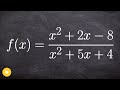
Understanding Functions and Discontinuities

The video tutorial explains how to analyze a rational function by factoring it to identify removable and non-removable discontinuities. It also covers how to find vertical and horizontal asymptotes, and determine the domain and range of the function. The instructor emphasizes the importance of factoring and provides a step-by-step approach to solving the problem.

What is the function given in the problem?

• x^2 - 2x - 8 / x^2 - 5x - 4

• x^2 - 2x + 8 / x^2 - 5x + 4

• x^2 + 2x - 8 / x^2 + 5x + 4

• x^2 + 2x + 8 / x^2 + 5x - 4

Why is factoring important in solving this problem?

• It simplifies the function for easier analysis.

• It changes the function to a polynomial.

• It eliminates the need for asymptotes.

• It makes the function continuous.

What is a removable discontinuity?

• A point where the function is undefined but can be canceled out.

• A point where the function is undefined and cannot be canceled out.

• A point where the function has a vertical asymptote.

• A point where the function is continuous.

Which value of x represents a removable discontinuity in this problem?

• x = 1

• x = -4

• x = 0

• x = -1

What is a non-removable discontinuity?

• A point where the function has a horizontal asymptote.

• A point where the function is continuous.

• A point where the function is undefined and cannot be canceled out.

• A point where the function is undefined but can be canceled out.

Which value of x represents a non-removable discontinuity in this problem?

• x = 1

• x = 0

• x = -1

• x = -4

What happens to the function at a removable discontinuity?

• The function has a vertical asymptote.

• The function becomes continuous.

• The function is undefined and cannot be simplified.

• The function is undefined but can be simplified.

How can a removable discontinuity be resolved?

• By factoring and canceling out the common factor.

• By adding a constant to the function.

• By multiplying the function by a constant.

• By setting the function equal to zero.

What is the vertical asymptote of the function?

• x = -1

• x = 1

• x = 0

• x = -4

What is the significance of a vertical asymptote?

• It indicates a non-removable discontinuity.

• It indicates a removable discontinuity.

• It indicates the function is continuous.

• It indicates the function has a horizontal asymptote.