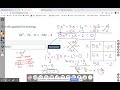
Trinomial Factoring and Zero Product Rule

This video tutorial covers the process of factoring trinomials when the leading coefficient (a) is greater than 1. It includes three detailed examples, demonstrating how to rearrange equations into standard form, use the generic rectangle and diamond method for factoring, and apply the zero product rule to solve for x. Each example is broken down into clear steps, highlighting the importance of identifying factors and using common factors to simplify the process.

What is the first step when solving a trinomial where the leading coefficient is greater than 1?

• Divide all terms by the leading coefficient

• Graph the equation

• Use the quadratic formula

• Rearrange the equation into standard form

When rearranging an equation into standard form, what should the equation be equal to?

• 1

• 0

• The leading coefficient

• The constant term

In the generic rectangle method, where do the first and last terms of the trinomial go?

• Diagonal from each other

• In the center of the rectangle

• Left and right of the rectangle

• Top and bottom of the rectangle

What is the purpose of the diamond method in trinomial factoring?

• To determine the greatest common factor

• To simplify the trinomial

• To identify the factors that multiply to the product of the first and last terms and add to the middle term

• To find the roots of the equation

How do you determine the greatest common factor (GCF) in the generic rectangle?

• By dividing the terms in each row and column

• By adding the terms in each row and column

• By finding the common factors of the coefficients and variables in each row and column

• By multiplying the terms in each row and column

What is the zero product rule used for in solving trinomials?

• To set each factor equal to zero and solve for the variable

• To divide the equation by zero

• To multiply the factors together

• To find the sum of the roots

In the second example, what is the first step to rearrange the equation into standard form?

• Subtract the x-term from both sides

• Divide all terms by the constant

• Multiply all terms by the leading coefficient

• Add the constant to both sides

What is the result of applying the zero product rule to the factored form of the second example?

• x = 1/2 and x = -4/3

• x = 2 and x = -3/2

• x = 3 and x = -2

• x = 0 and x = 1

In the third example, what is the first step to rearrange the equation into standard form?

• Subtract the constant from both sides

• Add the x-term to both sides

• Multiply all terms by the leading coefficient

• Divide all terms by the constant

What is the final solution for x in the third example after applying the zero product rule?

• x = 0 and x = 1

• x = 2 and x = -3/2

• x = 1/2 and x = -4/3

• x = 3 and x = -2