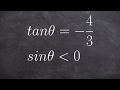
Trigonometric Functions and Triangle Analysis

The video tutorial addresses a problem involving the tangent of theta, initially misstated as negative 4 pi over 3, and corrects it to negative 4 over 3. The instructor explains the concept of tangent as y over x and discusses the two possible triangles that can be formed. The lesson then shifts to using Cartesian coordinates to visualize these triangles and applies constraints to determine the correct triangle to use. The instructor calculates the sine, cosine, and reciprocal functions, emphasizing the importance of understanding the constraints and the correct application of trigonometric identities.

What is the initial problem statement discussed in the video?

• Tangent of theta equals 4 pi over 3

• Cosine of theta equals negative 3 over 4

• Sine of theta equals 4 over 3

• Tangent of theta equals negative 4 over 3

What is the significance of having a negative tangent value?

• It shows the angle is greater than 90 degrees

• It means the angle is in the first quadrant

• It suggests the angle is on the unit circle

• It indicates two possible triangles

What is the relationship between tangent and the sides of a triangle?

• Tangent is the ratio of the opposite side to the adjacent side

• Tangent is the ratio of the hypotenuse to the adjacent side

• Tangent is the ratio of the hypotenuse to the opposite side

• Tangent is the ratio of the adjacent side to the hypotenuse

What is the purpose of drawing triangles in this context?

• To calculate the exact angle

• To find the sine value

• To visualize the problem and find possible solutions

• To determine the unit circle position

Why is it important to consider Cartesian coordinates in this context?

• To visualize the triangle orientation

• To find the sine value

• To determine the unit circle position

• To calculate the exact angle

In which quadrants is sine less than zero?

• Third and fourth quadrants

• Second and third quadrants

• First and fourth quadrants

• First and second quadrants

Why is only one triangle used for the final calculations?

• To simplify the calculations

• Because the other triangle is not a right triangle

• Because the other triangle is not valid

• Due to the constraint that sine is less than zero

What is the main reason for not using both triangles in the calculations?

• Because one triangle is not a right triangle

• To simplify the explanation

• Because one triangle is incorrect

• To avoid doing the problem twice

What is the significance of the constraint 'sine is less than zero'?

• It suggests the angle is on the unit circle

• It shows the angle is greater than 90 degrees

• It indicates the angle is in the first quadrant

• It helps determine the correct triangle to use

What is the main challenge discussed in the video?

• Finding the correct triangle with a negative tangent

• Calculating the exact angle

• Determining the unit circle position

• Finding the sine value