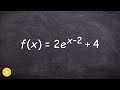
Exponential Functions Concepts Review

The video tutorial covers exponential functions, focusing on the constant 'e' and its application in continuous compounding. It explains the general form of exponential functions and how transformations like dilation and shifts affect their graphs. The tutorial also discusses graphing techniques, including using an xy table to determine points, and highlights the importance of understanding asymptotes and range. Finally, it demonstrates how to apply transformations to find new intercepts and asymptotes.

What is the general form of an exponential function?

• f(x) = a * b^(x-h) + k

• f(x) = ax^2 + bx + c

• f(x) = a * log_b(x-h) + k

• f(x) = a * sin(bx + c)

What does the base 'e' represent in exponential functions?

• A variable

• A constant representing continuous growth

• A transformation factor

• A coefficient

In the function f(x) = a * b^(x-h) + k, what does 'h' represent?

• Reflection point

• Vertical shift

• Horizontal shift

• Dilation factor

What is the y-intercept of the parent graph of an exponential function?

• (1, 1)

• (0, 1)

• (1, 0)

• (0, 0)

Why is an xy table useful in graphing exponential functions?

• It helps find the slope

• It determines the y-intercept

• It helps identify key points on the graph

• It calculates the asymptote

What happens to the graph of f(x) = 2e^(x-2) + 4 when it is transformed?

• It reflects over the x-axis

• It shifts right and up

• It becomes a linear function

• It shifts left and down

What is an asymptote in the context of exponential functions?

• A point where the graph crosses the x-axis

• A line that the graph approaches but never touches

• A point where the graph crosses the y-axis

• A line that the graph intersects at infinity

What is the domain of an exponential function?

• All positive numbers

• All integers

• All negative numbers

• All real numbers

Why is it important to apply extra points when graphing?

• To ensure accuracy in the graph's shape

• To find the maximum value

• To determine the slope

• To make the graph look more complex