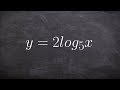
Logarithmic Functions and Their Properties

The video tutorial explains how to graph the function y = 2 log base 5 of X, focusing on understanding the domain and range rather than the exact graph shape. It discusses the effects of transformations like vertical stretch and compression, and how these do not affect the graph's position. The tutorial emphasizes the importance of visualizing the graph to determine the domain and range, noting that the graph approaches but does not cross zero, with a domain from zero to positive infinity and a range from negative to positive infinity.

What is the primary focus when graphing y = 2 log base 5 of X?

• Finding the exact graph shape

• Determining the domain and range

• Calculating the slope

• Identifying the x-intercept

How do transformations affect the graph of y = 2 log base 5 of X?

• They rotate the graph

• They do not affect the graph's position

• They change the graph's color

• They shift the graph left or right

What does the number 2 in y = 2 log base 5 of X do to the graph?

• It shifts the graph upwards

• It reflects the graph over the x-axis

• It compresses the graph horizontally

• It stretches the graph vertically

What is the effect of the base 5 in the logarithmic function?

• It compresses the graph vertically

• It shifts the graph to the right

• It makes the graph wider

• It sharpens the graph's turn

How does the graph of y = 2 log base 5 of X differ from y = log(x)?

• It is horizontally compressed

• It is vertically stretched

• It is shifted upwards

• It is shifted to the left

What is the role of the base in a logarithmic function?

• It determines the vertical stretch

• It affects the sharpness of the graph's turn

• It shifts the graph horizontally

• It changes the graph's color

What is the characteristic behavior of the parent graph y = log(x)?

• It approaches zero but never crosses it

• It is a straight line

• It crosses the y-axis

• It has a horizontal asymptote

What is the domain of the function y = 2 log base 5 of X?

• x < 0

• All real numbers

• x = 0

• x > 0

Why does the graph of y = 2 log base 5 of X never cross zero?

• Because it is a horizontal line

• Because it has an asymptote at zero

• Because it is a vertical line

• Because it is undefined at zero

How does the graph of y = 2 log base 5 of X behave as x approaches zero?

• It oscillates

• It increases indefinitely

• It decreases indefinitely

• It remains constant