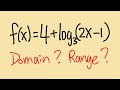
Logarithmic Functions and Their Properties

The video tutorial explains how to determine the domain and range of a logarithmic function. It begins by introducing the function 4 + log base 3 of (2x - 1) and highlights the importance of ensuring the inside of the logarithm is greater than zero. The domain is found by solving the inequality 2x - 1 > 0, resulting in x > 1/2. The range is discussed in terms of the graph's behavior, noting that it extends from negative infinity to positive infinity. The video also touches on the concept of vertical asymptotes and the absence of horizontal asymptotes in logarithmic functions.

What is the primary goal when analyzing the function 4 + log base 3 of (2x - 1)?

• To calculate its integral

• To determine its domain and range

• To solve for x

• To find its derivative

What must be true about the inside of a logarithmic function for its domain?

• It must be equal to zero

• It can be any real number

• It must be greater than zero

• It must be less than zero

How is the domain of the function 4 + log base 3 of (2x - 1) expressed in interval notation?

• (1/2, ∞)

• [1/2, ∞)

• (-∞, 1/2)

• (0, ∞)

What is the domain of the function 4 + log base 3 of (2x - 1) in terms of x?

• x < 0

• x > 1/2

• x > 0

• x < 1/2

Why can't the inside of a logarithmic function be zero?

• Because it would make the function undefined

• Because it would make the function negative

• Because it would make the function positive

• Because it would make the function zero

What is the primary difference between the domain of a logarithmic function and a square root function?

• Square root functions can have zero inside

• Square root functions can have negative inside

• Logarithmic functions can have negative inside

• Logarithmic functions can have zero inside

What happens when the inside of a logarithmic function equals zero?

• The function is undefined

• The function has a vertical asymptote

• The function has a horizontal asymptote

• The function equals zero

What is the behavior of the graph of a logarithmic function as it approaches its vertical asymptote?

• It remains constant

• It becomes undefined

• It approaches infinity

• It approaches zero

What is the significance of a vertical asymptote in the graph of a logarithmic function?

• It indicates where the function is zero

• It shows where the function is undefined

• It represents the minimum value of the function

• It marks the maximum value of the function

How does the graph of 4 + log base 3 of (2x - 1) differ from a standard logarithmic graph?

• It is shifted down four units

• It is shifted up four units

• It is reflected over the x-axis

• It is reflected over the y-axis