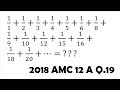
Prime Factorization and Geometric Series

The video tutorial explores a problem from the 2018 AMC 12 exam, focusing on numbers with prime factors 2, 3, and 5. It explains how to express the infinite sum of their reciprocals as a fraction M/N and find M plus N. The tutorial breaks down the problem by initially considering only factors 2 and 3, then extends the solution to include factor 5. It uses geometric series to simplify the calculation and concludes with the final answer.

What is the main focus of the problem discussed in the video?

• Numbers with prime factors 2, 5, or 7

• Numbers with prime factors 7, 11, or 13

• Numbers with prime factors 3, 5, or 11

• Numbers with prime factors 2, 3, or 5

What is the goal of the infinite sum discussed in the video?

• To express the sum as a decimal

• To find the product of all numbers

• To find the sum of all numbers

• To express the sum as a fraction M/N and find M + N

Which mathematical concept is used to solve the problem?

• Geometric series

• Arithmetic series

• Harmonic series

• Fibonacci sequence

Why is the problem initially simplified by considering only two prime factors?

• To make the problem more complex

• To focus on a smaller set of numbers

• To avoid using prime factor 5

• To make the problem easier to solve

What is the first step in evaluating the infinite geometric series for numbers with prime factors 2 and 3?

• Consider numbers with no prime factors

• Consider numbers with only prime factor 3

• Consider numbers with only prime factor 2

• Consider numbers with both prime factors 2 and 3

How is the solution extended to include numbers with prime factor 5?

• By dividing by a geometric series

• By ignoring the geometric series

• By subtracting a geometric series

• By adding another geometric series

What is the final answer to the problem?

• M/N = 15/4, M + N = 19

• M/N = 10/3, M + N = 13

• M/N = 20/5, M + N = 25

• M/N = 12/7, M + N = 19