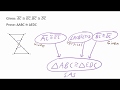
Understanding Geometry Proofs and Concepts

This video tutorial introduces flowchart thinking in geometry, focusing on using flowcharts to organize logical processes and prove triangle congruence. It covers the side-angle-side method, angle bisectors, and the role of parallel lines and alternate interior angles in proofs. The tutorial also demonstrates how to prove line segments congruent by establishing triangle congruence.

What is the primary purpose of a flowchart in geometry?

• To measure angles

• To solve algebraic equations

• To create artistic designs

• To organize a process in a logical order

How do flowcharts help in understanding geometric proofs?

• By offering multiple solutions

• By providing exact measurements

• By showing how facts lead to conclusions

• By simplifying complex equations

What should you do if given information is not marked on a diagram?

• Ask for more information

• Ignore it

• Mark it on the diagram

• Use a different proof method

Which congruence shortcut is used when two sides and the included angle are known?

• Angle-Angle-Side

• Side-Angle-Side

• Angle-Side-Angle

• Side-Side-Side

What is the role of an angle bisector in a flowchart proof?

• To find the midpoint of a segment

• To measure the length of a side

• To divide an angle into two congruent angles

• To create a perpendicular line

Why is it important to include all necessary statements in a proof?

• To add unnecessary details

• To ensure the proof is self-sufficient

• To make the proof longer

• To confuse the reader

What do alternate interior angles indicate when two lines are parallel?

• The angles are supplementary

• The angles are congruent

• The lines are perpendicular

• The lines are skew

How can you prove that two line segments are congruent using triangle congruence?

• By showing the triangles are congruent first

• By measuring the segments directly

• By assuming they are equal

• By using a ruler