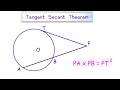
Tangent Secant Theorem Concepts

The video tutorial explains the tangent secant theorem, which states that the product of the lengths of a secant segment and its external segment is equal to the square of the length of the tangent segment. The video provides a detailed proof using angle-angle similarity of triangles and the alternate segment theorem. The tutorial concludes with a summary of the theorem and its proof.

What is the main focus of the Tangent Secant Theorem?

• The relationship between two secants.

• The relationship between a chord and a tangent.

• The relationship between a secant and a tangent.

• The relationship between two tangents.

According to the Tangent Secant Theorem, what is the product of the lengths PA and PB equal to?

• The square of PA.

• The difference between PT and PA.

• The sum of PT and PB.

• The square of PT.

In the diagram, which line represents the tangent?

• The yellow line.

• The green line.

• The red line.

• The blue line.

What is the first step in proving the Tangent Secant Theorem?

• Identifying the center of the circle.

• Calculating the length of the tangent.

• Drawing a perpendicular from the center.

• Joining specific points to form triangles.

Which theorem is used to establish the angle relationships in the proof?

• Sine Rule.

• Pythagorean Theorem.

• Alternate Segment Theorem.

• Angle Bisector Theorem.

What is the common angle in triangles PBT and PTA?

• Angle at point A.

• Angle at point B.

• Angle at point P.

• Angle at point T.

How are the triangles PBT and PTA proven to be similar?

• By having equal areas.

• By having equal sides.

• By having equal angles.

• By having equal perimeters.

What is the significance of the angle angle similarity in the proof?

• It determines the length of the tangent.

• It proves the circle's diameter.

• It establishes the similarity of triangles.

• It helps in calculating the area of the circle.

Which part of the circle does the chord BT subtend an angle on?

• The secant line.

• The remaining part of the circle.

• The tangent line.

• The center of the circle.

What is the relationship between PB and PT in the proof?

• PB is twice PT.

• PB is proportional to PT.

• PB is half of PT.

• PB is equal to PT.