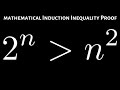
Mathematical Induction Concepts

The video tutorial demonstrates how to prove that 2^N is greater than N^2 for N greater than 4 using mathematical induction. It begins with an introduction to the problem, followed by proving the base case for N = 5. The induction hypothesis assumes the statement is true for some K greater than 4. The induction step involves proving the statement for N = K + 1. Finally, the proof is concluded by confirming the statement is true for all N greater than 4 using the principle of mathematical induction.

What is the main goal of the video tutorial?

• To demonstrate the use of mathematical induction

• To explain the concept of limits

• To prove that 2^N is less than N^2 for N greater than 4

• To solve a quadratic equation

What is the base case in the induction proof discussed?

• N = 4

• N = 6

• N = 5

• N = 1

Why is the base case important in an induction proof?

• It proves the statement for all integers

• It establishes the truth of the statement for the smallest integer

• It is not necessary for the proof

• It simplifies the problem

What assumption is made in the induction hypothesis?

• 2^K is equal to K^2 for some K greater than 4

• 2^K is greater than K^2 for some K greater than 4

• 2^K is greater than K^2 for all K

• 2^K is less than K^2 for some K greater than 4

What is the purpose of the induction step in the proof?

• To simplify the equation

• To find the value of K

• To prove the statement for K + 1 assuming it is true for K

• To verify the base case

How is 2^(K+1) expressed in terms of 2^K?

• 2^(K+1) = 2^K / 2

• 2^(K+1) = 2^K - 1

• 2^(K+1) = 2 * 2^K

• 2^(K+1) = 2^K + 1

What algebraic trick is used to simplify 2^(K+1)?

• Dividing exponents

• Multiplying exponents

• Adding exponents

• Subtracting exponents

What is the final conclusion of the proof?

• The statement is true for N = 5 only

• The statement is true for N = 4 only

• The statement is false for all positive integers

• The statement is true for all positive integers greater than 4

What is the principle used to conclude the proof?

• Principle of Contradiction

• Principle of Mathematical Induction

• Principle of Least Action

• Principle of Sufficient Reason

What is the significance of proving the statement for K + 1?

• It is not significant

• It simplifies the equation

• It verifies the base case

• It shows the statement is true for all integers