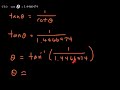
Trigonometric Functions and Calculations

This lesson focuses on using calculators to approximate trigonometric function values for angles, emphasizing the importance of setting calculators to degree mode. It covers calculating tangent and cosine values, using reciprocal identities for functions like cosecant and secant, and finding angles with inverse trigonometric functions. The lesson concludes with practical applications, such as calculating grade resistance for vehicles on inclines.

Why is it important to set the calculator to degree mode when evaluating trigonometric functions of angles given in degrees?

• To avoid syntax errors.

• To ensure the calculator interprets angles correctly.

• To make calculations faster.

• To save battery life.

What should you do if your calculator does not have a button for inputting degrees, minutes, and seconds directly?

• Convert minutes to a decimal by dividing by 60.

• Convert the angle to radians first.

• Use a different calculator.

• Ignore the minutes and only input degrees.

In which quadrant is the angle 193.600 degrees located?

• Quadrant III

• Quadrant II

• Quadrant I

• Quadrant IV

How can you calculate the cosecant of an angle if your calculator does not have a cosecant button?

• Use the reciprocal of the secant function.

• Use the reciprocal of the cosine function.

• Use the reciprocal of the tangent function.

• Use the reciprocal of the sine function.

What is the inverse function used to find an angle when given the cosine value?

• Inverse sine

• Inverse cotangent

• Inverse cosine

• Inverse tangent

What does a negative grade resistance indicate when calculating for a vehicle on a slope?

• The vehicle is accelerating.

• The vehicle is stationary.

• The vehicle is moving downhill.

• The vehicle is moving uphill.