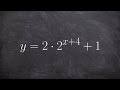
Graphing Exponential Functions and Transformations

The video tutorial explains how to graph an equation by initially ignoring constants and focusing on the base equation. It then demonstrates how to apply transformations, such as shifting the graph left, right, up, or down, and adjusting the horizontal asymptote. The tutorial concludes with regraphing the equation after transformations and ensuring the graph's shape is correct.

What is the first step in graphing the equation y = 2 * 2^x?

• Shift the graph horizontally.

• Ignore the y-intercept.

• Graph it as y = 2 * 2^x using a table.

• Consider the transformations first.

Why is it important to use a table when graphing y = 2 * 2^x?

• To find the x-intercept.

• To determine the slope.

• To accurately plot points and understand the y-intercept.

• To calculate the derivative.

What does adding 4 to the x-value in the equation do to the graph?

• Shifts the graph 4 units to the right.

• Shifts the graph 4 units to the left.

• Moves the graph 4 units down.

• Moves the graph 4 units up.

How does adding 1 to the equation affect the graph?

• It shifts the graph 1 unit to the right.

• It shifts the graph 1 unit down.

• It shifts the graph 1 unit to the left.

• It shifts the graph 1 unit up.

What is the new position of the y-intercept after the transformations?

• 4 units left and 1 unit up.

• 4 units right and 1 unit down.

• 4 units right and 1 unit up.

• 4 units left and 1 unit down.

What happens to the horizontal asymptote after a vertical shift of 1 unit up?

• It disappears.

• It remains at y = 0.

• It moves to y = -1.

• It moves to y = 1.

What is the original position of the horizontal asymptote before any transformations?

• y = 0

• y = 1

• y = 2

• y = -1

What is the effect of a vertical transformation on the graph's asymptote?

• It has no effect.

• It changes the slope.

• It alters the x-intercept.

• It shifts the horizontal asymptote vertically.

What is the significance of the y-intercept in graph transformations?

• It determines the slope.

• It changes the x-intercept.

• It is the starting point for vertical shifts.

• It has no significance.

What is the role of the horizontal asymptote in graph transformations?

• It changes the graph's shape.

• It acts as a boundary for vertical shifts.

• It determines the graph's slope.

• It is irrelevant to transformations.