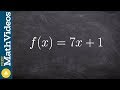
Verifying Inverses and Function Composition
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Practice Problem
•
Hard
Thomas White
FREE Resource
Read more
7 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the primary purpose of verifying inverses?
To ensure the functions are bijective
To confirm the functions are linear
To check if the functions are continuous
To validate that the functions are inverses of each other
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How can inverses be described in terms of operations?
As operations that square and square root
As operations that switch domain and range
As operations that multiply and divide
As operations that add and subtract
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of composing a function with its inverse?
The inverse function
A constant function
The identity element
The original function
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the example with f(x) = x + 1, what is the inverse function?
f inverse(x) = x + 1
f inverse(x) = x - 1
f inverse(x) = x * 1
f inverse(x) = x / 1
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What happens when you compose two functions that are not inverses?
You get the identity element
You do not get the identity element
You get the original function
You get a constant function
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the identity element in the context of function composition?
The function f(x)
The variable x
The number 0
The number 1
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why is it important to verify inverses using composition?
To validate the functions are linear
To check if the functions are differentiable
To confirm the functions are inverses
To ensure the functions are continuous
Similar Resources on Wayground

11 questions
Sine Function Concepts and Applications
Interactive video
•
9th - 12th Grade

11 questions
Understanding Linear Algebra
Interactive video
•
9th - 12th Grade

11 questions
Direct and Inverse Variation Concepts
Interactive video
•
9th - 10th Grade

11 questions
Understanding Functions and Their Properties
Interactive video
•
9th - 10th Grade

11 questions
Bone Health and Osteoporosis Concepts
Interactive video
•
9th - 10th Grade

11 questions
Understanding Coordinate Systems and Transformations
Interactive video
•
9th - 12th Grade

11 questions
Understanding Level Curves
Interactive video
•
9th - 12th Grade

11 questions
Understanding the Continuity Equation
Interactive video
•
9th - 12th Grade
Popular Resources on Wayground

5 questions
This is not a...winter edition (Drawing game)
Quiz
•
1st - 5th Grade

25 questions
Multiplication Facts
Quiz
•
5th Grade

10 questions
Identify Iconic Christmas Movie Scenes
Interactive video
•
6th - 10th Grade

20 questions
Christmas Trivia
Quiz
•
6th - 8th Grade

18 questions
Kids Christmas Trivia
Quiz
•
KG - 5th Grade

11 questions
How well do you know your Christmas Characters?
Lesson
•
3rd Grade

14 questions
Christmas Trivia
Quiz
•
5th Grade

20 questions
How the Grinch Stole Christmas
Quiz
•
5th Grade
Discover more resources for Mathematics

10 questions
Identify Iconic Christmas Movie Scenes
Interactive video
•
6th - 10th Grade

33 questions
Algebra 1 Semester 1 Final 2025
Quiz
•
8th - 10th Grade

10 questions
Exploring Global Holiday Traditions
Interactive video
•
6th - 10th Grade

10 questions
Guess the Christmas Movie by the Scene Challenge
Interactive video
•
6th - 10th Grade

10 questions
Guess the Christmas Songs Challenge
Interactive video
•
6th - 10th Grade

20 questions
Function or Not a Function
Quiz
•
8th - 9th Grade

10 questions
Test Your Christmas Trivia Skills
Interactive video
•
6th - 10th Grade

15 questions
Holiday Trivia!
Quiz
•
9th Grade