What is the main focus of the video tutorial?
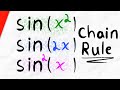
Chain Rule and Derivatives
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Hard
Thomas White
FREE Resource
Read more
18 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Graphing trigonometric functions
Integrating complex functions
Differentiating simple functions using the chain rule
Solving algebraic equations
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which functions are being differentiated in the video?
Cosine of 2x, cosine of x squared, and cosine squared of X
Exponential of 2x, exponential of x squared, and exponential squared of X
Sine of 2x, sine of x squared, and sine squared of X
Tangent of 2x, tangent of x squared, and tangent squared of X
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the derivative of the outside function when differentiating sine of 2x?
Secant
Cosine
Sine
Tangent
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the derivative of the inside function in sine of 2x?
0
1
x
2
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the final derivative of sine of 2x?
2 cosine of 2x
2 sine of x
sine of 2x
cosine of x
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the derivative of sine of x squared, what is the outside function?
Tangent
Exponential
Cosine
Sine
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the derivative of the inside function in sine of x squared?
0
2x
1
x
Create a free account and access millions of resources
Similar Resources on Quizizz

16 questions
Analyzing Tangent Line Slopes
Interactive video
•
9th - 10th Grade

11 questions
Stationary Points and Sine Functions
Interactive video
•
9th - 10th Grade

16 questions
Eliminating Theta in Parametric Equations
Interactive video
•
9th - 10th Grade

11 questions
Geometry and Trigonometry Problem Solving
Interactive video
•
9th - 10th Grade

11 questions
Trigonometric Concepts and Applications
Interactive video
•
9th - 10th Grade

16 questions
Trigonometric Identities and Simplifications
Interactive video
•
9th - 10th Grade

14 questions
Calculus Derivatives and Integrals
Interactive video
•
9th - 10th Grade

11 questions
Understanding Derivatives and Trigonometric Functions
Interactive video
•
9th - 10th Grade
Popular Resources on Quizizz

15 questions
Multiplication Facts
Quiz
•
4th Grade

20 questions
Math Review - Grade 6
Quiz
•
6th Grade

20 questions
math review
Quiz
•
4th Grade

5 questions
capitalization in sentences
Quiz
•
5th - 8th Grade

10 questions
Juneteenth History and Significance
Interactive video
•
5th - 8th Grade

15 questions
Adding and Subtracting Fractions
Quiz
•
5th Grade

10 questions
R2H Day One Internship Expectation Review Guidelines
Quiz
•
Professional Development

12 questions
Dividing Fractions
Quiz
•
6th Grade