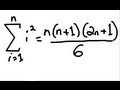
Telescoping Sums and Sum of Squares

The video tutorial explains the sum of squares of integers and introduces the telescoping sum method. It provides a detailed proof of the telescoping sum and demonstrates its application in solving mathematical problems. An example calculation is shown using the proven formula, illustrating the method's effectiveness.

What is the formula for the sum of squares of the first n positive integers?

• n(n + 1)(n + 2)/6

• n(n + 1)/2

• n^2

• n(n + 1)(2n + 1)/6

What is a telescoping sum?

• A sum where terms cancel each other out

• A sum of consecutive integers

• A sum of squares

• A sum of cubes

In a telescoping sum, what happens to most of the terms?

• They cancel out

• They are squared

• They double

• They remain unchanged

What is the result of expanding (n + 1)^3 - 1^3?

• n^3 + 4n^2 + 4n

• n^3 + 3n^2 + 3n

• n^3 + n^2 + n

• n^3 + 2n^2 + n

How can the telescoping sum be rewritten using Sigma notation?

• As a sum of squares

• As a sum of cubes

• As a sum of differences

• As a sum of products

What is the final step in proving the sum of squares formula?

• Guessing the result

• Using a calculator

• Calculating the sum manually

• Equating two forms of the telescoping sum

What is the sum of squares for n = 4 using the formula?

• 30

• 20

• 25

• 35