Arc Length and Circular Geometry

The video tutorial explains a problem involving two cars racing on a circular track with a diameter of one mile. The cars are positioned 89 degrees apart, and the task is to calculate how far car B must travel to reach car A's current location. The tutorial emphasizes the importance of drawing a diagram to visualize the problem. It introduces the arc length formula, s = R * theta, where R is the radius and theta is the angle in radians. The video demonstrates converting degrees to radians and performs the final calculation, resulting in a distance of 0.78 miles.

What is the initial problem presented in the video?

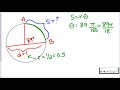
• Two cars racing on a square track

• Two cars racing on a triangular track

• Two cars racing on a circular track

• Two cars racing on a straight track

Why is it suggested to draw a picture for this problem?

• To make the problem more colorful

• To better visualize and understand the problem

• To make the problem more difficult

• To avoid using any formulas

What is the diameter of the circular track?

• Two miles

• One mile

• Half a mile

• Three miles

What is the relationship between diameter and radius?

• Radius is twice the diameter

• Diameter is half the radius

• Radius is half the diameter

• Diameter is twice the radius

What is the angle between car A and car B in degrees?

• 45 degrees

• 90 degrees

• 89 degrees

• 180 degrees

What is the formula used to calculate the arc length?

• s = R + theta

• s = R - theta

• s = R / theta

• s = R * theta

What does the letter 's' represent in the arc length formula?

• Time

• Arc length

• Distance

• Speed

What is the first step in using the arc length formula?

• Convert the radius to degrees

• Convert the angle to radians

• Convert the radius to miles

• Convert the diameter to radians

What is the purpose of converting degrees to radians in this problem?

• To make the problem more complex

• To avoid using a calculator

• To use the arc length formula correctly

• To simplify the problem

What is the angle in radians used in the calculation?

• 180 pi over 89

• 89 pi over 360

• 89 pi over 180

• 89 degrees