Chord and Circle Geometry Concepts

The video tutorial discusses a geometry problem involving two concentric circles with a chord of the outer circle acting as a tangent to the inner circle. The problem is solved using both mathematical and logical approaches. The mathematical approach involves applying the Pythagorean theorem to find the area of the shaded region, while the logical approach demonstrates how the area remains constant regardless of changes in the radii of the circles. The solution concludes with a summary of the findings.

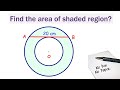
What is the length of the chord AB in the problem?

• 15 cm

• 10 cm

• 20 cm

• 25 cm

In the context of the problem, what role does the chord AB play with respect to the inner circle?

• It is a secant

• It is a diameter

• It is a tangent

• It is a radius

What is the significance of the chord being a tangent to the inner circle?

• It means the chord is parallel to the radius

• It means the chord is equal to the radius

• It means the chord is a diameter

• It means the chord is perpendicular to the radius

What theorem is applied to solve the problem mathematically?

• Binomial Theorem

• Thales' Theorem

• Pythagorean Theorem

• Fermat's Last Theorem

What is the relationship between the radii of the circles and the chord in the mathematical approach?

• The radii are parallel

• The radii form a right triangle with half the chord

• The radii are perpendicular

• The radii are equal

What is the area of the shaded region in terms of pi?

• 50π

• 100π

• 125π

• 75π

What is the result of applying the Pythagorean theorem in this problem?

• R^2 = r^2 + 5^2

• R^2 = r^2 + 20^2

• R^2 = r^2 + 10^2

• R^2 = r^2 - 10^2

What is the role of point M in the mathematical approach?

• It is the tangential point on the inner circle

• It is the endpoint of the chord

• It is the midpoint of the chord

• It is the center of the outer circle

How does changing the radius of the outer circle affect the shaded region?

• It doubles the area

• It increases the area

• It decreases the area

• The area remains the same

What happens to the shaded region if the inner circle's radius is reduced to zero?

• It halves

• It doubles

• It becomes the area of a circle with radius 10 cm

• It disappears