What is the initial step in converting Cartesian coordinates to polar coordinates?
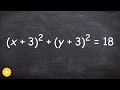
Polar Coordinates and Related Concepts
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Hard
Thomas White
FREE Resource
Read more
15 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Replace x with r sin(theta) and y with r cos(theta)
Replace x with r cos(theta) and y with r sin(theta)
Replace x with r tan(theta) and y with r cot(theta)
Replace x with r sec(theta) and y with r csc(theta)
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why is squaring binomials considered challenging in the context of polar coordinates?
It requires differentiation
It involves expanding terms which can be cumbersome
It requires integration
It involves complex numbers
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the correct way to expand (x + 3)^2?
x^2 + 3
x^2 + 9
x^2 + 6x + 9
x^2 + 3x + 3
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why is it important to understand the expansion of binomials?
To solve linear equations
To simplify trigonometric identities
To correctly convert expressions to polar form
To solve differential equations
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the purpose of grouping x squared and y squared terms?
To simplify the equation
To rewrite the equation in terms of polar coordinates
To eliminate variables
To factor the equation
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result of grouping terms with x squared and y squared?
A trigonometric identity
An equation in polar form
A quadratic equation
A linear equation
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why can't the r terms be combined in the polar form equation?
They are both quadratic
They are not like terms
They are both constants
They are both linear
Create a free account and access millions of resources
Similar Resources on Quizizz

11 questions
Understanding Polar Plots and Functions
Interactive video
•
9th - 10th Grade

11 questions
Complex Numbers and Polar Coordinates
Interactive video
•
9th - 10th Grade

11 questions
Polar Coordinates and Trigonometric Functions
Interactive video
•
9th - 10th Grade

10 questions
Graphing and Analyzing Rose Curves
Interactive video
•
9th - 10th Grade

14 questions
Intersection of Polar Curves
Interactive video
•
9th - 10th Grade

11 questions
Polar Coordinates and Trigonometric Functions
Interactive video
•
9th - 10th Grade

10 questions
Understanding Polar Graphs and Equations
Interactive video
•
9th - 10th Grade

11 questions
Complex Numbers and Their Properties
Interactive video
•
9th - 10th Grade
Popular Resources on Quizizz

15 questions
Multiplication Facts
Quiz
•
4th Grade

20 questions
Math Review - Grade 6
Quiz
•
6th Grade

20 questions
math review
Quiz
•
4th Grade

5 questions
capitalization in sentences
Quiz
•
5th - 8th Grade

10 questions
Juneteenth History and Significance
Interactive video
•
5th - 8th Grade

15 questions
Adding and Subtracting Fractions
Quiz
•
5th Grade

10 questions
R2H Day One Internship Expectation Review Guidelines
Quiz
•
Professional Development

12 questions
Dividing Fractions
Quiz
•
6th Grade