What is the primary focus of the video tutorial?
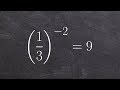
Converting Exponential and Logarithmic Forms
Interactive Video
•
Mathematics
•
9th - 10th Grade
•
Hard
Thomas White
FREE Resource
Read more
15 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Converting between exponential and logarithmic forms
Learning about calculus derivatives
Solving quadratic equations
Understanding trigonometric identities
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which formula is used to convert from logarithmic to exponential form?
b^y = x
x = log_b(y)
y = b^x
y = log(x)
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the equivalent of b^y = x in logarithmic form?
log_y(b) = x
log_b(x) = y
log_b(y) = x
log_x(b) = y
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the first step in solving these conversion problems?
Calculate the logarithm
Identify the exponent
Identify the base
Solve for x
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the base of the logarithm when converting from exponential form?
The power
The base of the exponent
The result
The exponent
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the relationship between the base of the exponent and the base of the logarithm?
They are the same
They are different
One is half the other
One is double the other
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the first thing to identify when converting an exponential equation?
The logarithm
The exponent
The base
The result
Create a free account and access millions of resources
Similar Resources on Quizizz

11 questions
Logarithmic Concepts and Properties
Interactive video
•
9th - 10th Grade

11 questions
Understanding Logarithms and Natural Logarithm Concepts
Interactive video
•
9th - 10th Grade

11 questions
Solving Exponential Equations and Logarithms
Interactive video
•
9th - 10th Grade

11 questions
Limits of Exponential and Logarithmic Functions
Interactive video
•
9th - 10th Grade

11 questions
Logarithmic Equations and Properties
Interactive video
•
9th - 10th Grade

11 questions
Logarithmic Equations and Properties
Interactive video
•
9th - 10th Grade

11 questions
Limits of Exponential and Logarithmic Functions
Interactive video
•
9th - 10th Grade

12 questions
Logarithm Concepts and Applications
Interactive video
•
9th - 10th Grade
Popular Resources on Quizizz

15 questions
Multiplication Facts
Quiz
•
4th Grade

20 questions
Math Review - Grade 6
Quiz
•
6th Grade

20 questions
math review
Quiz
•
4th Grade

5 questions
capitalization in sentences
Quiz
•
5th - 8th Grade

10 questions
Juneteenth History and Significance
Interactive video
•
5th - 8th Grade

15 questions
Adding and Subtracting Fractions
Quiz
•
5th Grade

10 questions
R2H Day One Internship Expectation Review Guidelines
Quiz
•
Professional Development

12 questions
Dividing Fractions
Quiz
•
6th Grade