
10 T
6th - 7th

10 T
7th

50 T
7th

12 T
5th - 7th

29 T
7th - 8th

32 T
7th

15 T
7th

21 T
7th - 8th

12 T
7th
10 T
5th - 8th

10 T
1st - 12th

19 T
7th

45 T
7th

20 T
7th

23 T
7th - 8th

10 T
7th

11 T
7th

10 T
7th

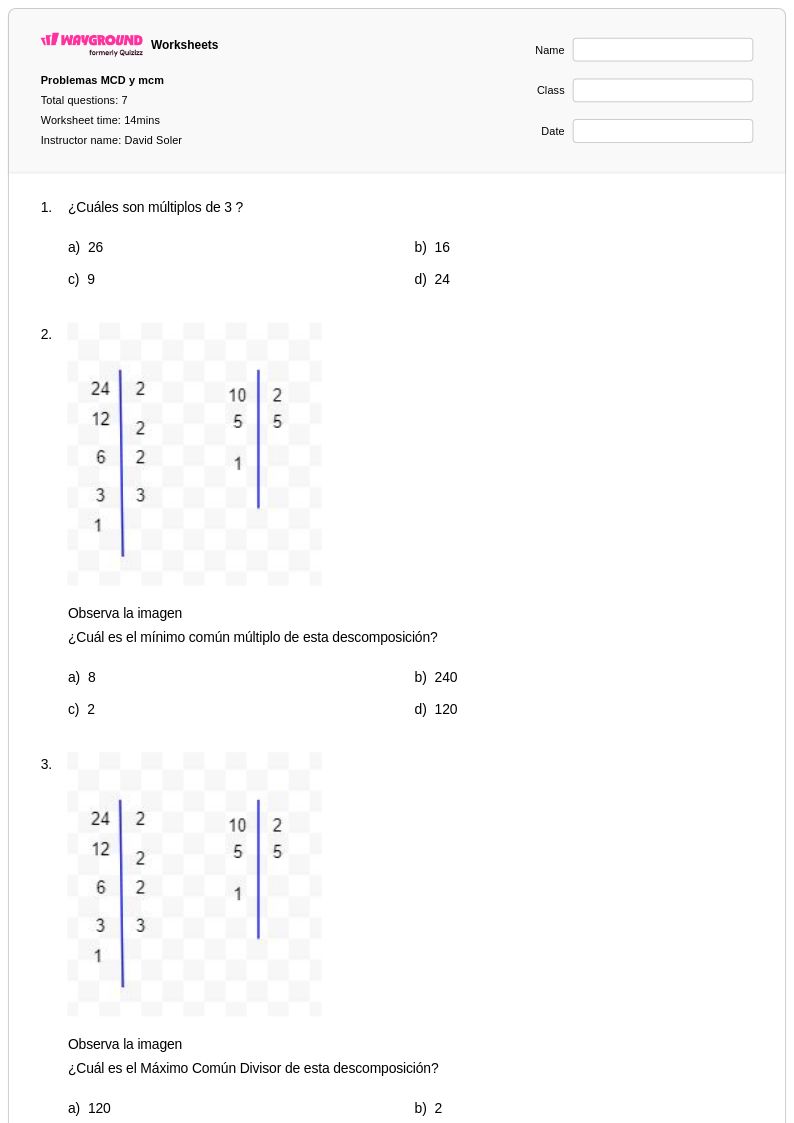
20 T
7th
7 T
7th - 8th

11 T
5th - 8th

49 T
7th

10 T
7th

20 T
7th
Jelajahi Máximo común divisor (MCD) Lembar Kerja berdasarkan Nilai
Jelajahi Lembar Kerja Mata Pelajaran Lainnya untuk grado 7
Explore las hojas de trabajo imprimibles de Máximo común divisor (MCD) para Grado 7
Las hojas de trabajo de Máximo Común Divisor para estudiantes de 7.º grado, disponibles a través de Wayground (anteriormente Quizizz), ofrecen una práctica integral en uno de los conceptos más fundamentales de la teoría de números. Estas hojas de trabajo, cuidadosamente diseñadas, ayudan a los estudiantes a dominar el proceso sistemático de hallar el mayor entero positivo que divide dos o más números sin residuo, fortaleciendo su comprensión de la divisibilidad, la factorización prima y el razonamiento matemático. Los estudiantes resuelven problemas de práctica progresivamente desafiantes que abarcan múltiples métodos para determinar el MCD, incluyendo la enumeración de factores, el uso de árboles de factorización prima y la aplicación del algoritmo de Euclides. Cada hoja de trabajo incluye claves de respuestas detalladas y soluciones paso a paso, lo que las convierte en valiosos recursos para el estudio independiente, las tareas y la enseñanza en el aula. Disponibles como imprimibles gratuitos en un práctico formato PDF, estos materiales son compatibles tanto con entornos de aprendizaje digitales como con la práctica tradicional en papel.
La extensa colección de hojas de trabajo de Máximo Común Divisor de Wayground se basa en millones de recursos creados por docentes, lo que proporciona a los educadores una selección inigualable de materiales alineados con los estándares de matemáticas de 7.º grado. Las funciones avanzadas de búsqueda y filtrado de la plataforma permiten a los docentes encontrar rápidamente hojas de trabajo que se ajusten a los objetivos de aprendizaje específicos, los niveles de habilidad de los estudiantes y las necesidades de instrucción. Las herramientas de diferenciación integradas permiten a los educadores personalizar la complejidad del contenido, modificar los conjuntos de problemas y crear rutas de aprendizaje personalizadas para actividades de refuerzo o enriquecimiento. Ya sea que se acceda digitalmente a través de formatos interactivos o se descarguen como hojas de trabajo PDF imprimibles, estos recursos se integran a la perfección en los flujos de trabajo de planificación de clases. Los docentes pueden identificar eficazmente materiales que abordan aplicaciones específicas del MFC, desde problemas básicos de dos números hasta problemas complejos de varios pasos que involucran situaciones del mundo real, lo que garantiza el desarrollo integral de habilidades y la fluidez matemática en diversos estilos de aprendizaje y niveles de preparación académica.
