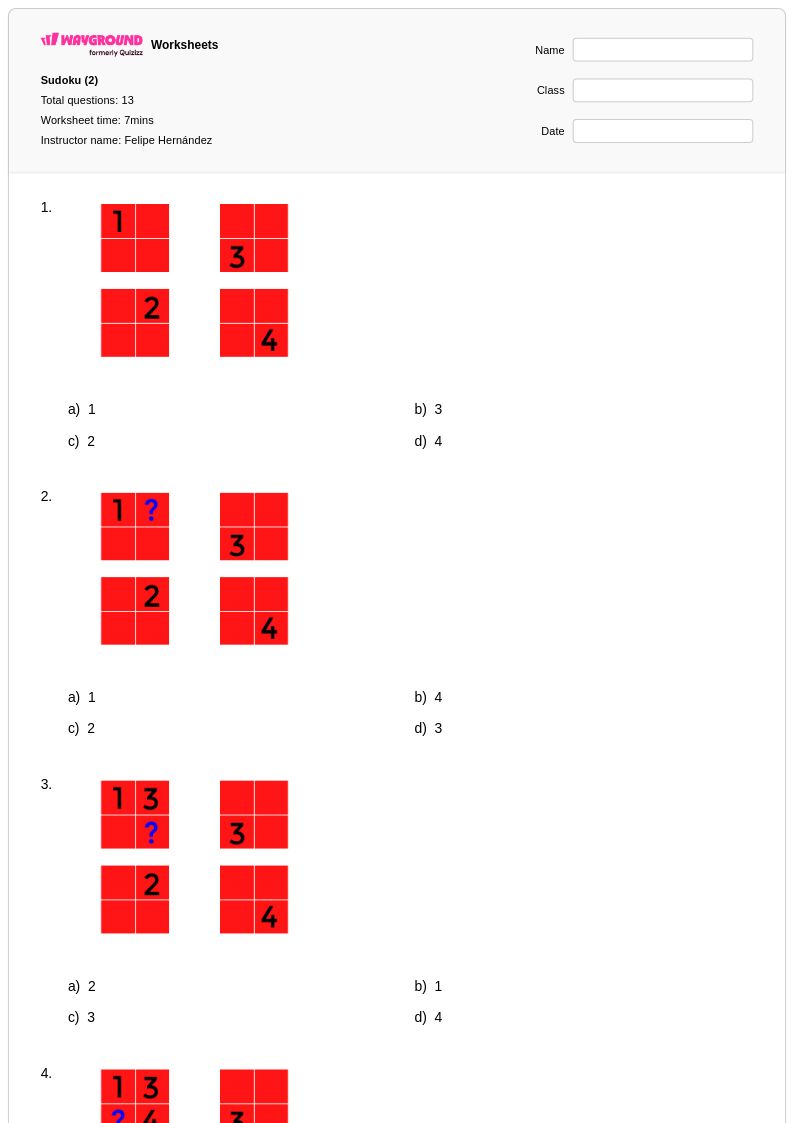
13 Q
1st - 2nd
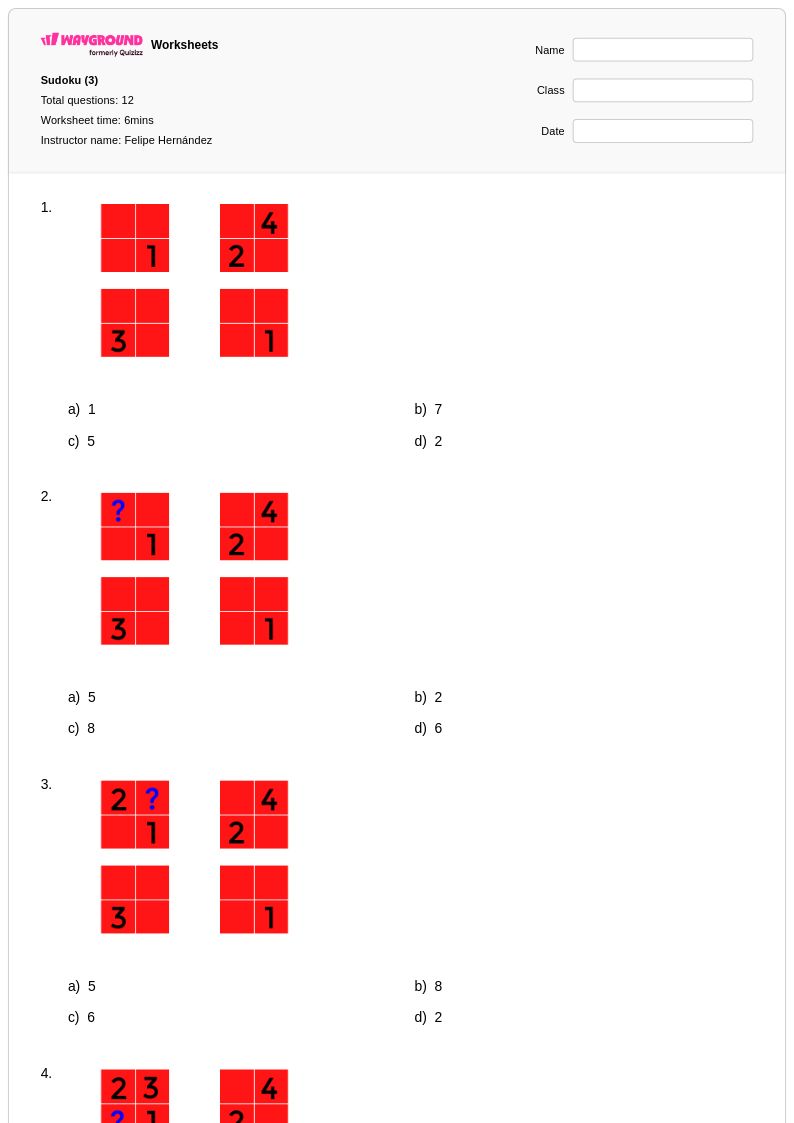
12 Q
1st - 2nd

5 Q
KG
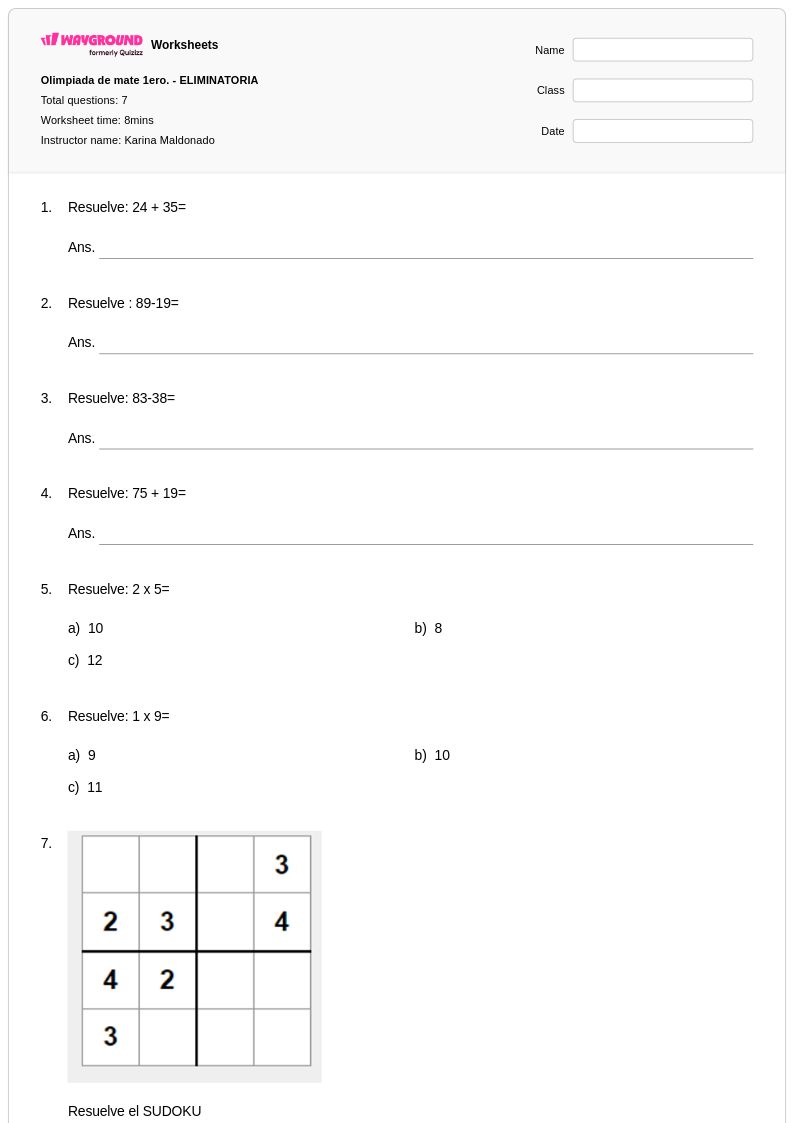
7 Q
1st

15 Q
9th - 12th

5 Q
Uni

6 Q
6th - 8th

6 Q
4th
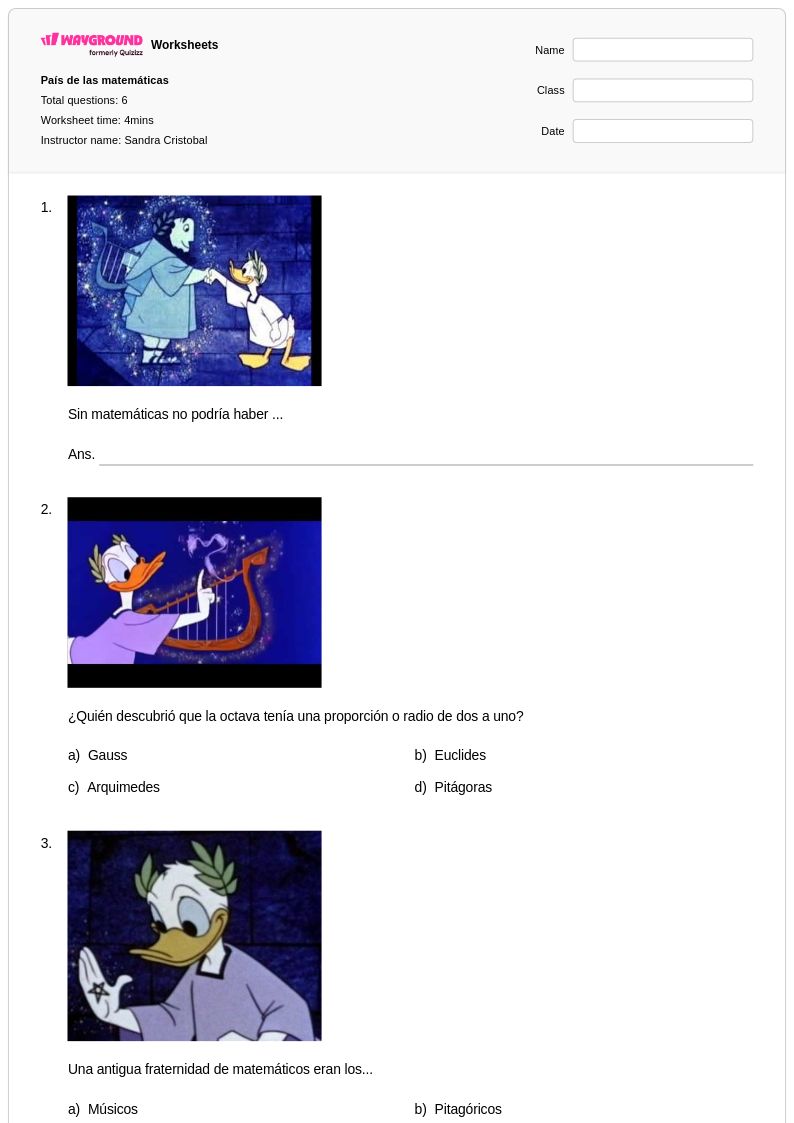
6 Q
1st

8 Q
1st - 3rd

5 Q
1st - 5th

7 Q
1st - 3rd

8 Q
1st - 3rd

7 Q
1st - 3rd

7 Q
1st - 3rd

9 Q
2nd
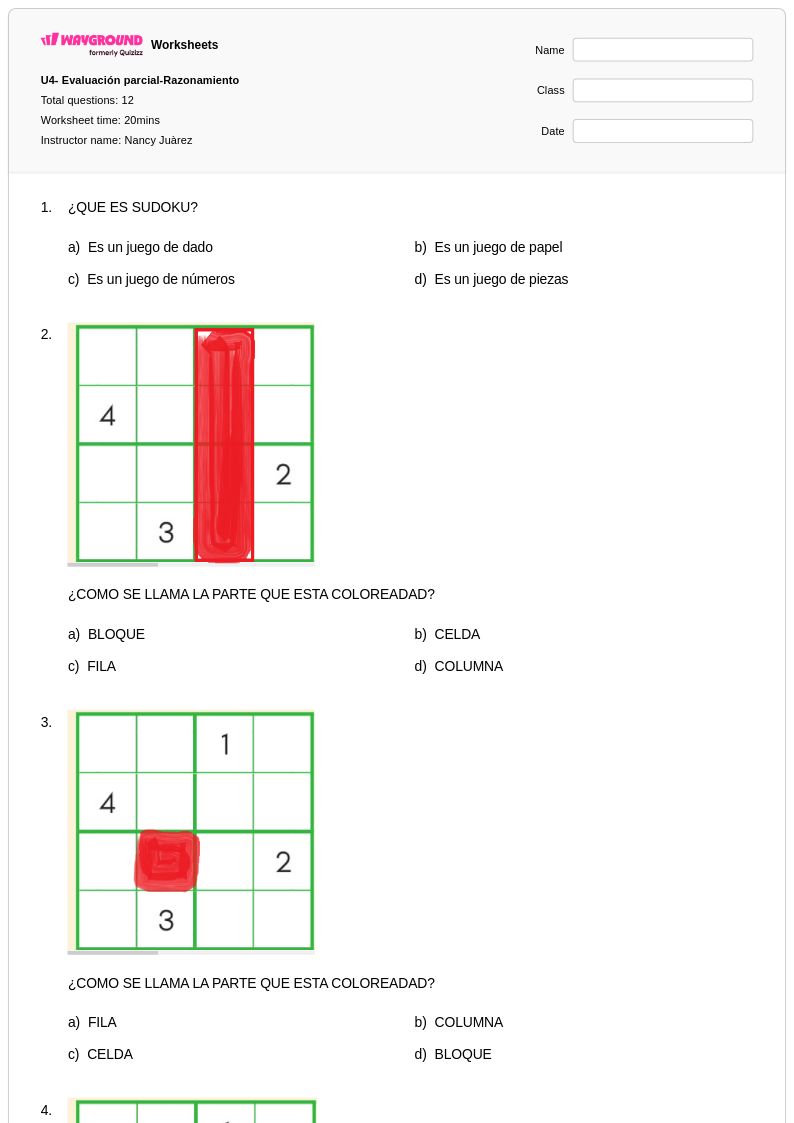
12 Q
8th

14 Q
5th

10 Q
1st - 11th
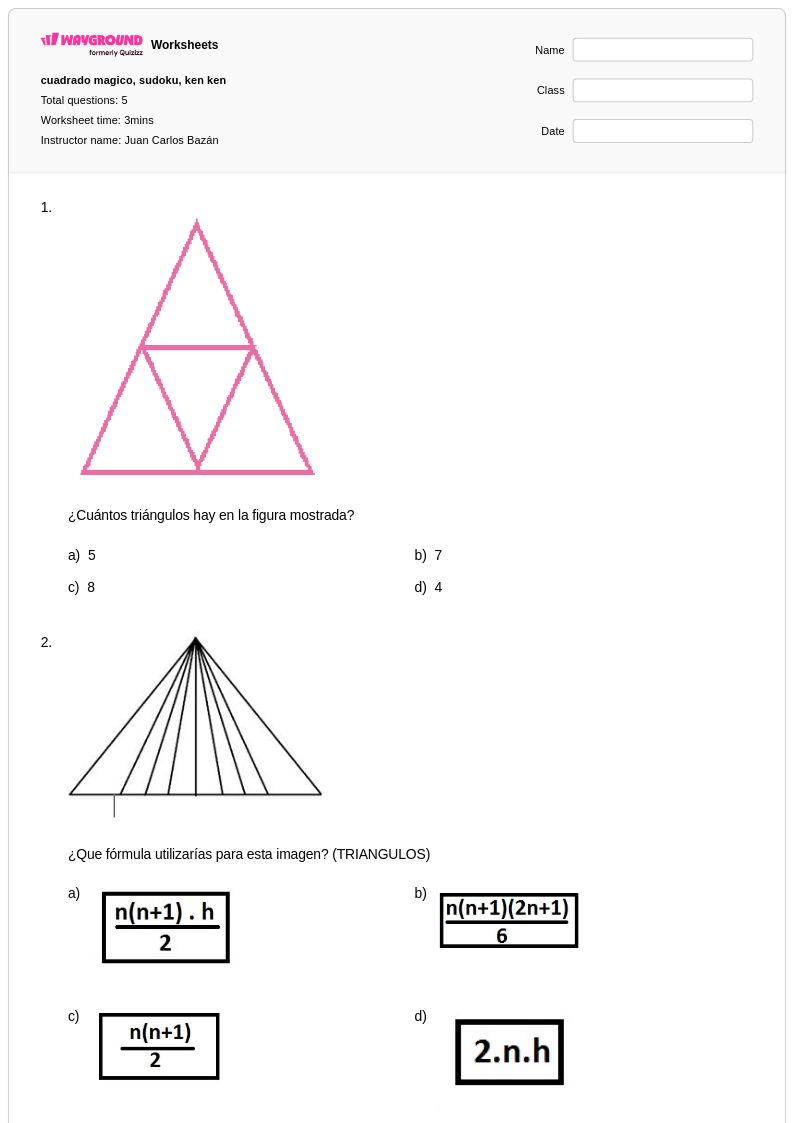
5 Q
9th

8 Q
8th
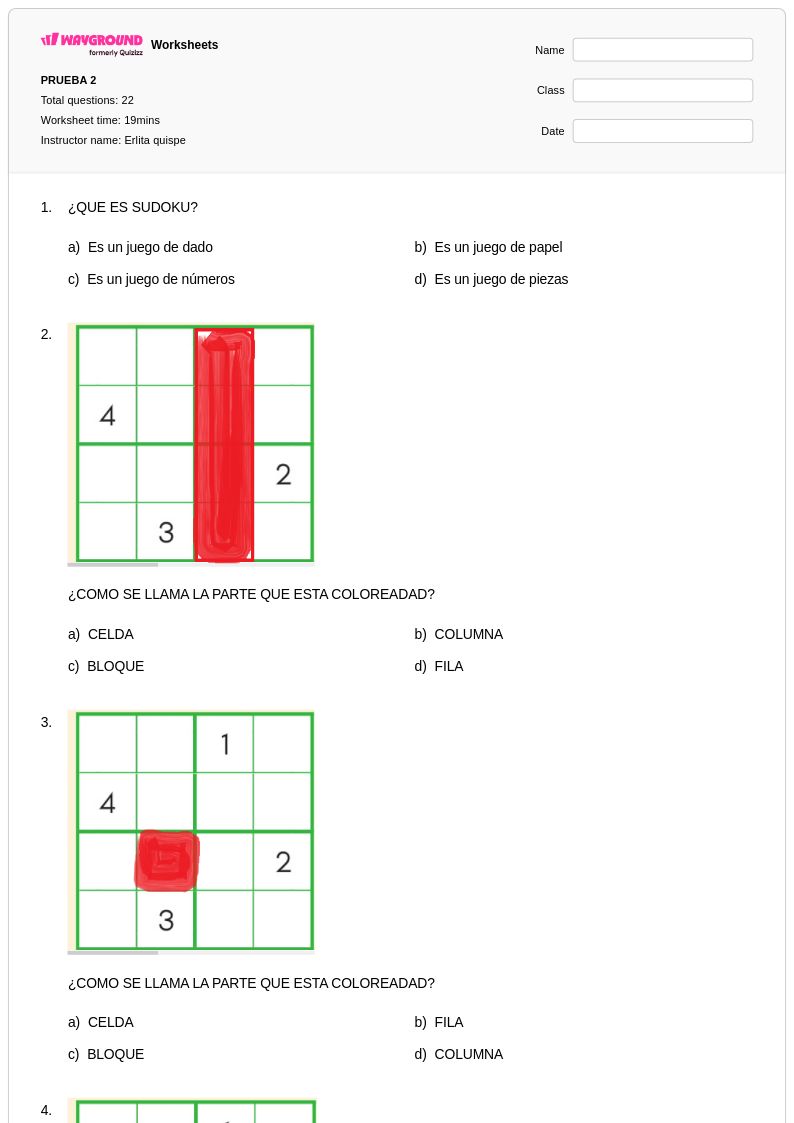
22 Q
5th

24 Q
9th

10 Q
1st - 10th
Explore Worksheets by Grade
Explore Worksheets by Subjects
Explore las hojas de trabajo imprimibles de Sudoku
Las hojas de ejercicios de Sudoku disponibles en Wayground (anteriormente Quizizz) ofrecen a los estudiantes interesantes desafíos de rompecabezas numéricos que desarrollan el pensamiento crítico, el razonamiento lógico y la resolución sistemática de problemas. Estos ejercicios, cuidadosamente diseñados, abarcan desde cuadrículas de 4x4 para principiantes hasta rompecabezas avanzados de 9x9. Cada uno requiere que los estudiantes apliquen el razonamiento deductivo y el reconocimiento de patrones para llenar cada fila, columna y casilla con números únicos. La completa colección incluye formatos PDF imprimibles con claves de respuestas completas, lo que facilita a los educadores implementar estos acertijos matemáticos gratuitos en el aula o asignarlos como práctica independiente para fortalecer el pensamiento analítico y el sentido numérico de los estudiantes.
Wayground (anteriormente Quizizz) ofrece a los docentes millones de recursos de Sudoku creados por ellos mismos que satisfacen diversas necesidades de aprendizaje mediante potentes funciones de búsqueda y filtrado, lo que permite identificar rápidamente rompecabezas que se ajustan a niveles de dificultad y estándares matemáticos específicos. Las herramientas de diferenciación de la plataforma permiten a los instructores personalizar la complejidad de los rompecabezas y el tamaño de las cuadrículas para adaptarse a diferentes niveles de habilidad, mientras que las opciones de formato flexibles ofrecen versiones tanto imprimibles como digitales para una integración perfecta en los planes de clase. Estas colecciones integrales de hojas de trabajo facilitan la práctica de habilidades específicas, sirven como herramientas de recuperación efectivas para estudiantes que tienen dificultades con el razonamiento lógico y ofrecen oportunidades de enriquecimiento para estudiantes avanzados, lo que hace que la planificación de lecciones sea más eficiente y al mismo tiempo garantiza que cada estudiante pueda acceder a experiencias de acertijos matemáticos desafiantes de manera adecuada.
