
15 Q
9th - Uni

10 Q
12th

10 Q
8th - 12th

31 Q
8th - 12th

8 Q
9th - 12th
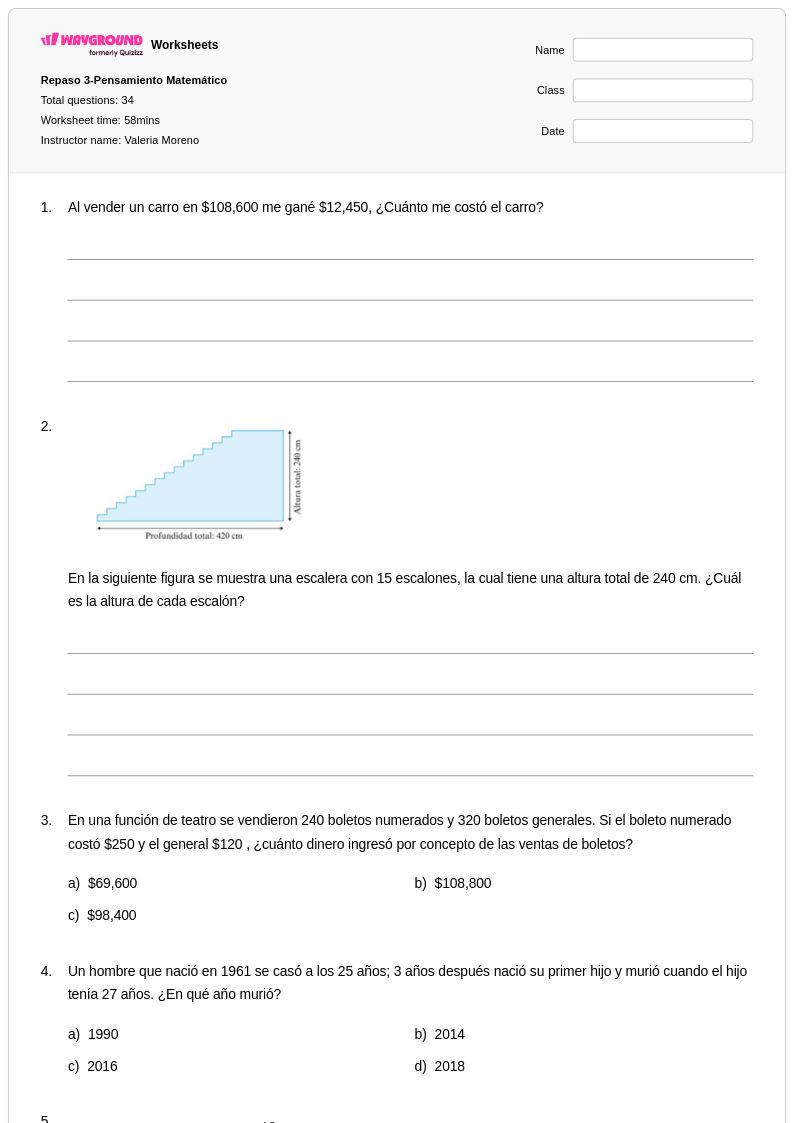
34 Q
12th

13 Q
12th

8 Q
10th - 12th

15 Q
8th - 12th
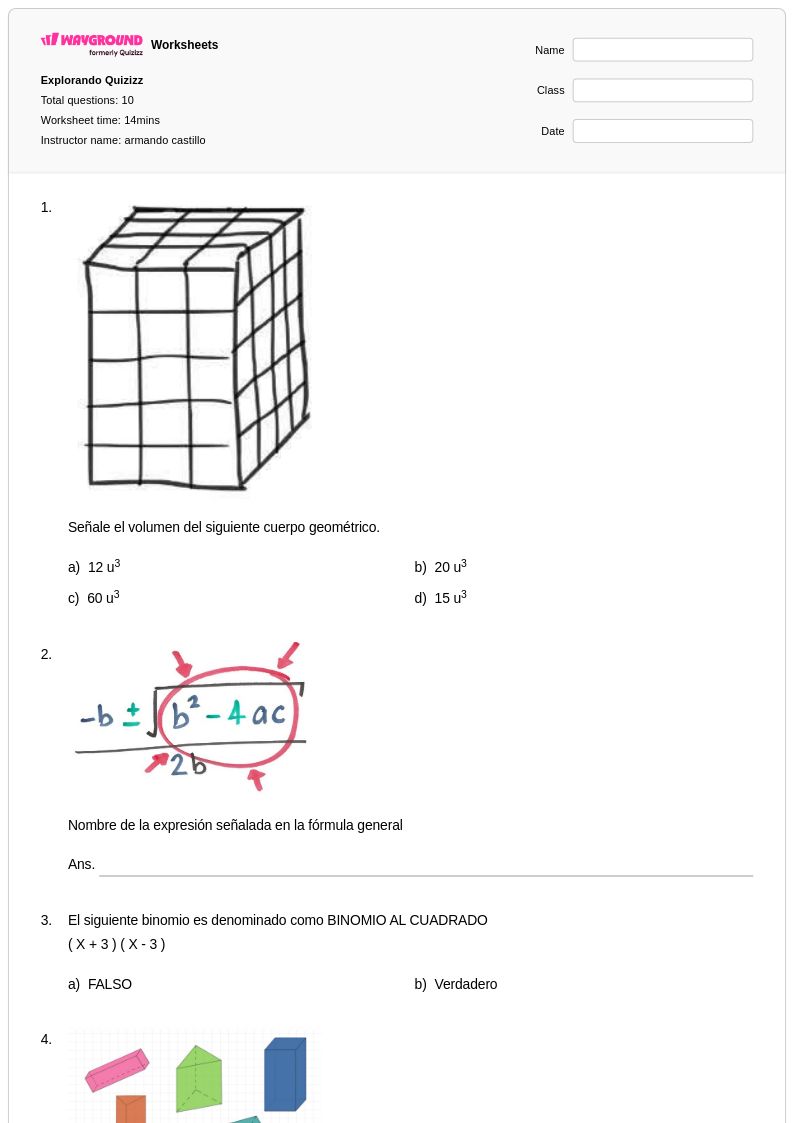
10 Q
7th - Uni

25 Q
2nd - 12th

10 Q
9th - 12th
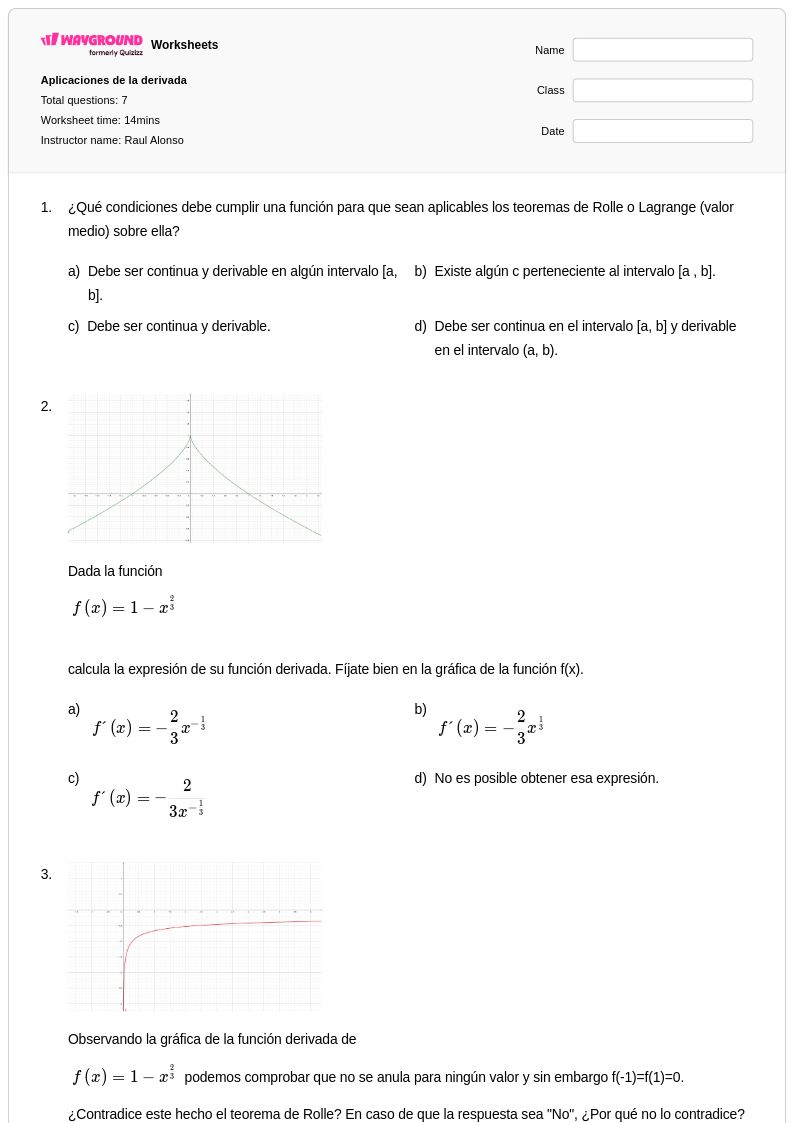
7 Q
12th

85 Q
12th

15 Q
12th
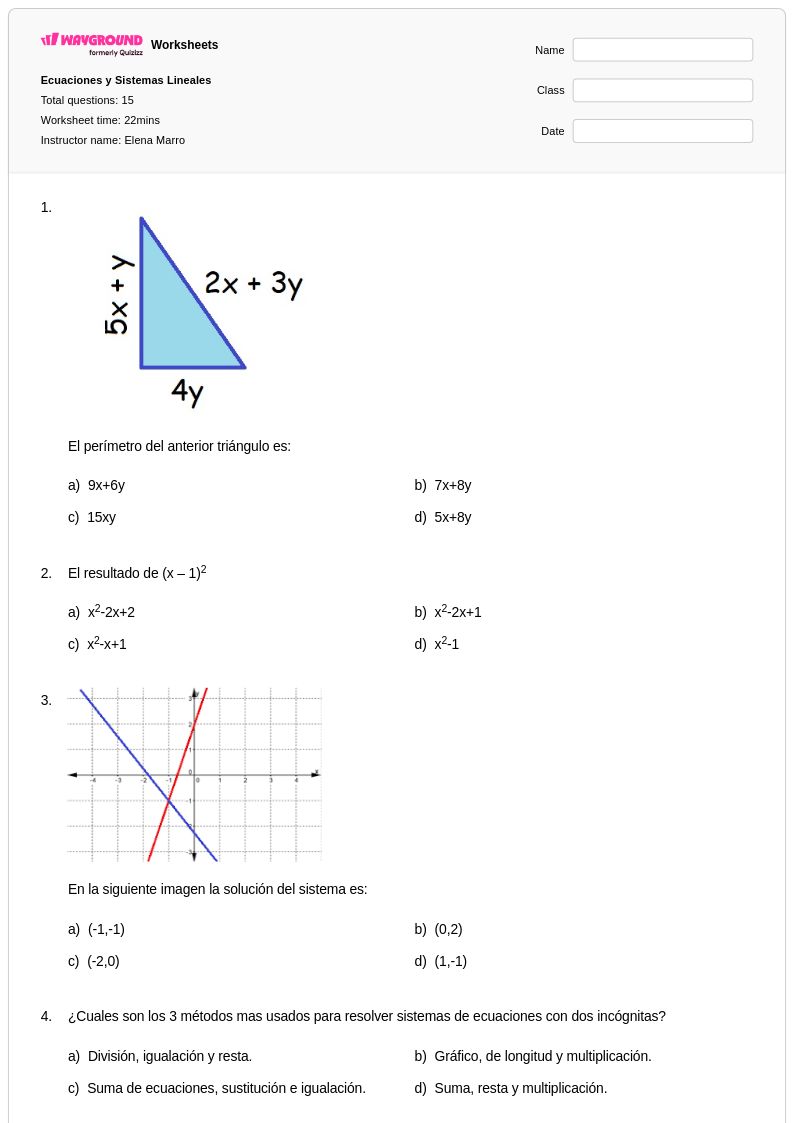
15 Q
KG - PD

21 Q
12th

62 Q
12th
10 Q
7th - Uni

5 Q
12th
7 Q
12th

16 Q
12th

10 Q
12th

22 Q
9th - 12th
Explore Other Subject Worksheets for grado 12
Explore las hojas de trabajo imprimibles de Teorema del binomio para Grado 12
Las hojas de trabajo del Teorema del Binomio para estudiantes de 12.º grado, disponibles a través de Wayground, ofrecen una práctica completa con uno de los conceptos matemáticos más importantes del álgebra. Estos recursos, diseñados por expertos, ayudan a los estudiantes a dominar el desarrollo de expresiones binomiales, comprender los patrones de triángulos de Pascal y aplicar coeficientes binomiales en situaciones algebraicas complejas. Cada colección de hojas de trabajo incluye claves de respuestas detalladas y está disponible como imprimibles gratuitos en un práctico formato PDF, lo que permite a los estudiantes resolver problemas de práctica que amplían progresivamente su comprensión de los desarrollos binomiales, la identificación de términos generales y las aplicaciones prácticas de este teorema fundamental.
La extensa biblioteca de recursos del Teorema del Binomio de Wayground, creada por docentes, se nutre de millones de materiales educativos y ofrece potentes funciones de búsqueda y filtrado que ayudan a los educadores a encontrar rápidamente contenido apropiado para su grado y alineado con los estándares matemáticos. Los docentes pueden diferenciar fácilmente la instrucción seleccionando entre varios niveles de dificultad y tipos de problemas, mientras que las flexibles herramientas de personalización de la plataforma permiten realizar modificaciones para satisfacer las necesidades específicas del aula. Disponibles en formatos imprimibles y digitales, incluidos archivos PDF descargables, estas colecciones de hojas de trabajo respaldan la planificación eficaz de lecciones, la recuperación específica para estudiantes con dificultades, las oportunidades de enriquecimiento para estudiantes avanzados y la práctica constante de habilidades que refuerza el razonamiento matemático necesario para el éxito en cursos avanzados de álgebra y cálculo.
