
16Q
12th

27Q
12th

12Q
12th
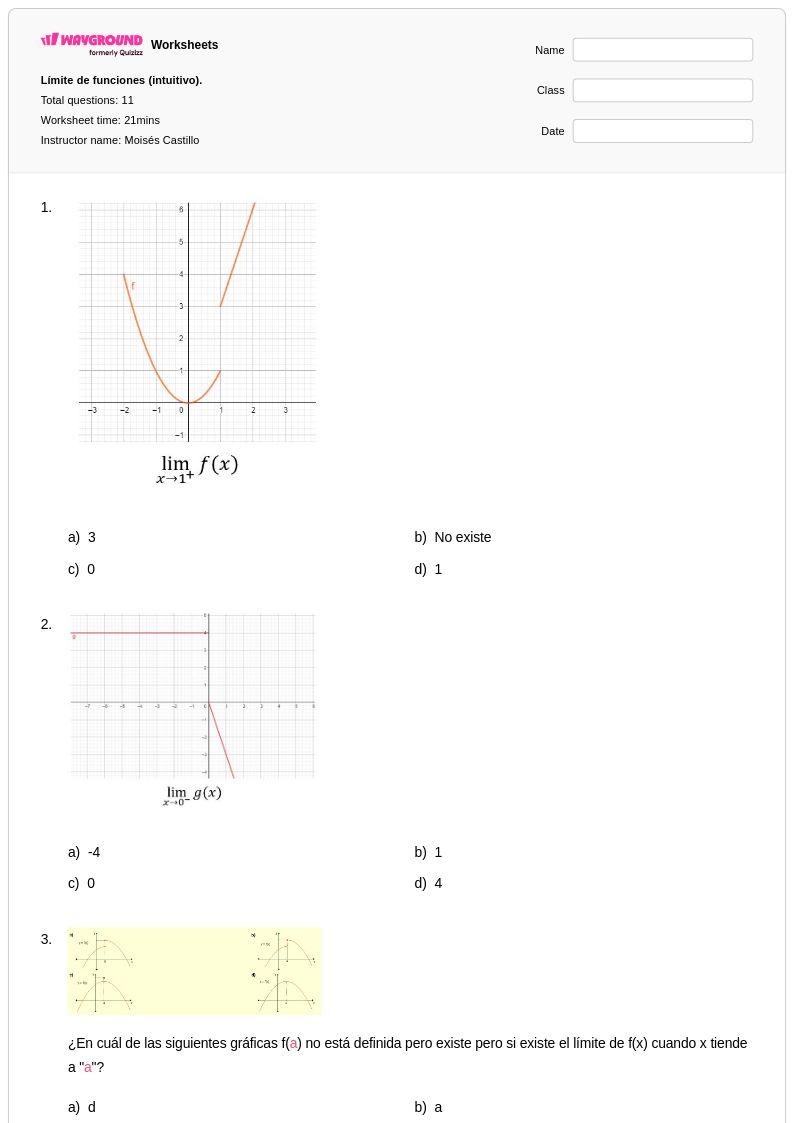
11Q
12th

7Q
1st - Uni

10Q
12th
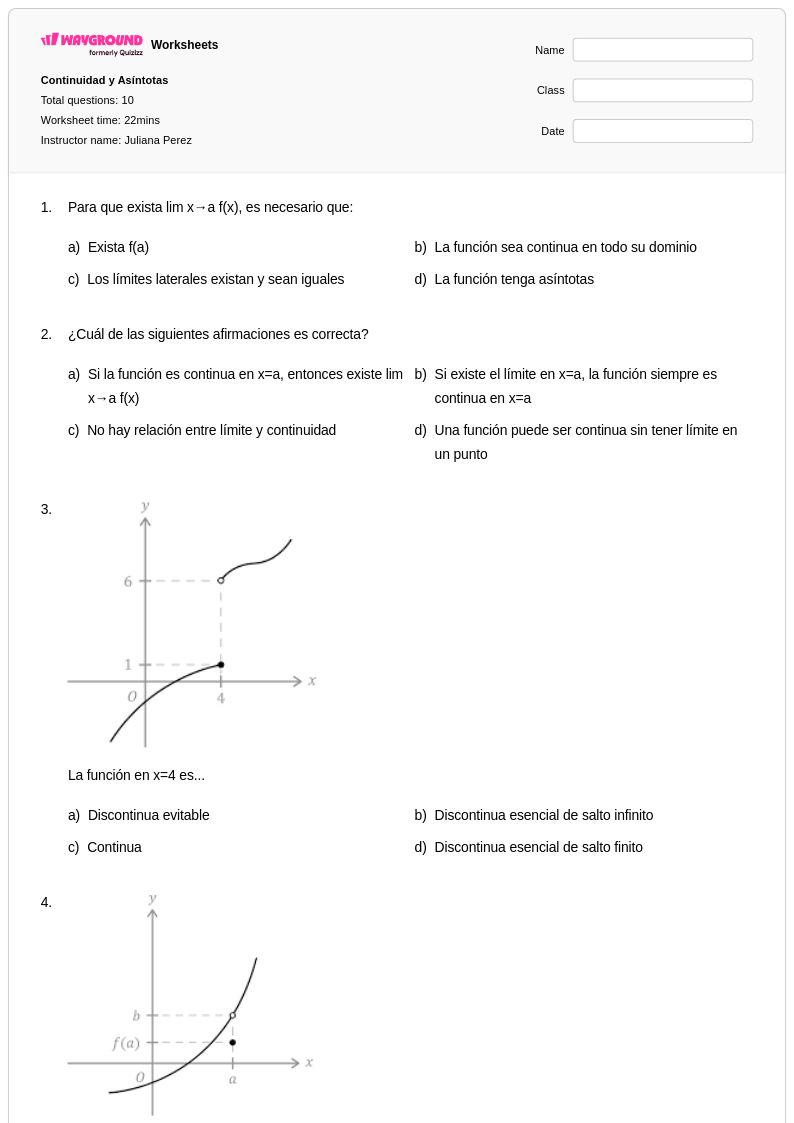
10Q
9th - 12th

17Q
12th

5Q
12th
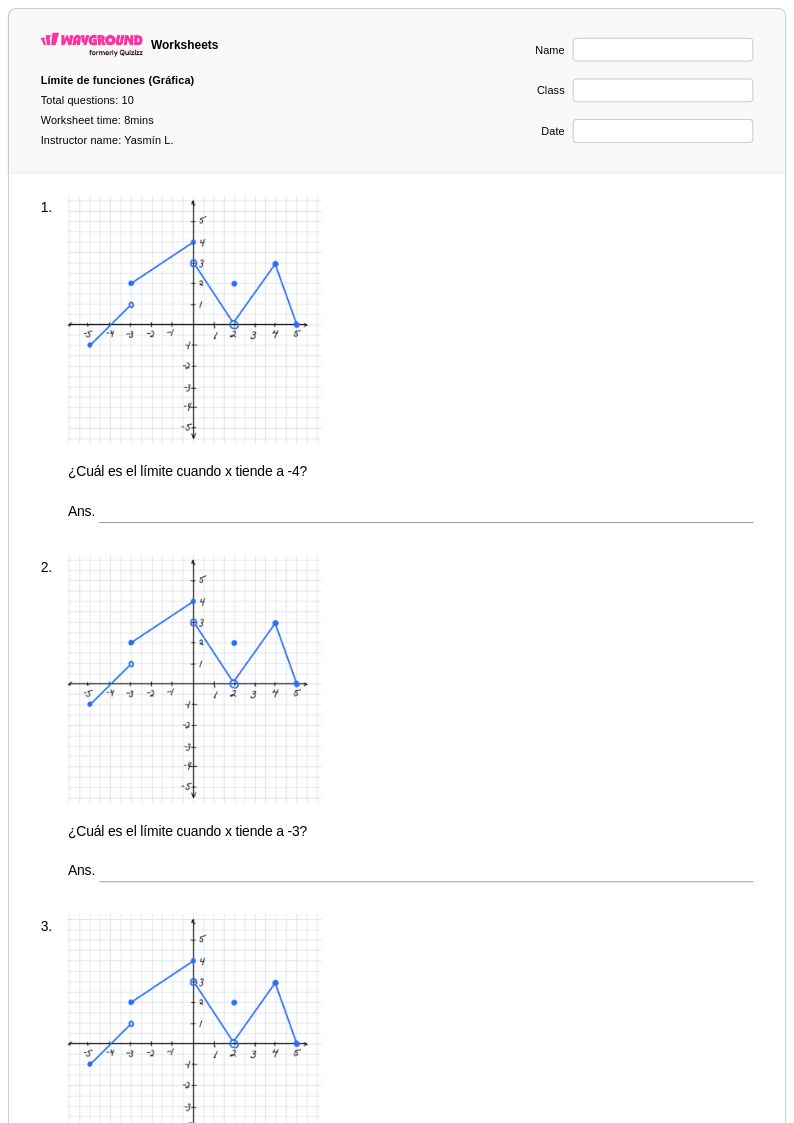
10Q
12th
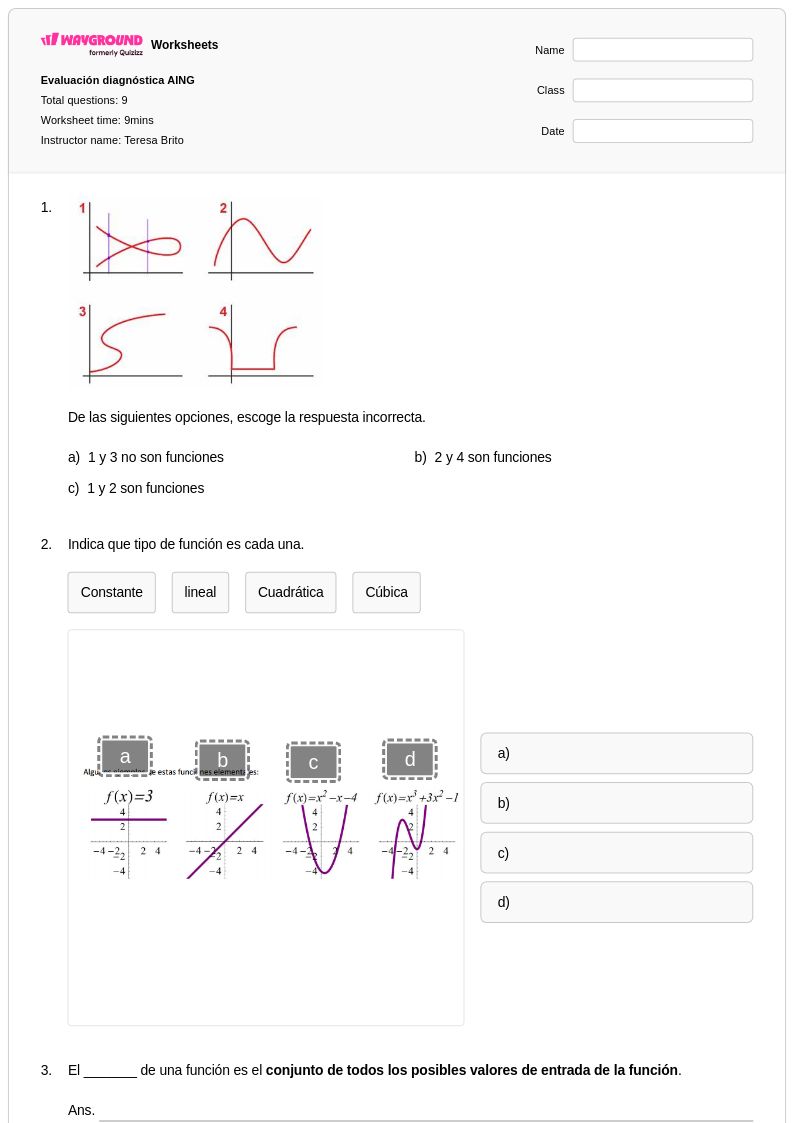
9Q
12th
24Q
12th

40Q
12th

13Q
9th - 12th

10Q
9th - 12th

6Q
12th

10Q
12th

14Q
12th

5Q
12th

15Q
12th

11Q
4th - Uni
11Q
12th

10Q
12th

13Q
12th
Explore otras hojas de trabajo de materias para grado 12
Explore las hojas de trabajo imprimibles de Límite de error de Lagrange para Grado 12
Las hojas de trabajo de Límites de Error de Lagrange para estudiantes de 12.º grado ofrecen práctica esencial con una de las herramientas analíticas más sofisticadas del cálculo para aproximar valores de funciones y comprender la precisión de las aproximaciones con polinomios de Taylor. Estas completas hojas de trabajo guían a estudiantes de matemáticas avanzadas en la aplicación sistemática del teorema de Lagrange para determinar los límites de error máximo al utilizar series de Taylor para aproximar funciones complejas. Los estudiantes desarrollan habilidades críticas para hallar derivadas de órdenes superiores, identificar intervalos apropiados para el análisis de errores y calcular límites precisos que garantizan la precisión de las aproximaciones polinomiales. Los recursos imprimibles gratuitos incluyen claves de respuestas detalladas que muestran soluciones paso a paso para determinar los límites de error en diversos tipos de funciones, desde funciones exponenciales y logarítmicas hasta expresiones trigonométricas. Los ejercicios de práctica progresan sistemáticamente desde aplicaciones básicas con polinomios simples hasta escenarios desafiantes que involucran funciones compuestas y series infinitas, asegurando que los estudiantes dominen tanto las técnicas computacionales como la comprensión conceptual de la teoría de aproximación.
Wayground, anteriormente Quizizz, ofrece a los profesores de matemáticas de 12.º grado una extensa colección de millones de hojas de trabajo de Límites de Error de Lagrange, creadas por ellos mismos, que agilizan la enseñanza y la evaluación del cálculo avanzado. Las robustas funciones de búsqueda y filtrado de la plataforma permiten a los educadores localizar rápidamente recursos alineados con estándares curriculares específicos, ya sea centrados en cálculos básicos de límites de error o en aplicaciones complejas que involucran teoremas de estimación de residuo. Los profesores se benefician de sofisticadas herramientas de diferenciación que permiten personalizar los niveles de dificultad de las hojas de trabajo, los tipos de problemas y la complejidad matemática para satisfacer las diversas necesidades de los estudiantes en cursos de nivel avanzado y de preparación para la universidad. Disponibles tanto en formato PDF imprimible como en versiones digitales interactivas, estos recursos facilitan la planificación flexible de lecciones para la enseñanza presencial, las tareas y las sesiones de refuerzo específicas. Las completas claves de respuestas y guías de soluciones de la plataforma facilitan la calificación eficiente, a la vez que proporcionan a los profesores explicaciones detalladas que pueden utilizar para repasar conceptos complejos, facilitando la resolución de malentendidos individuales de los estudiantes sobre el análisis de errores y la precisión de aproximación en temas de cálculo avanzado.
