
21Q
11th

10Q
11th
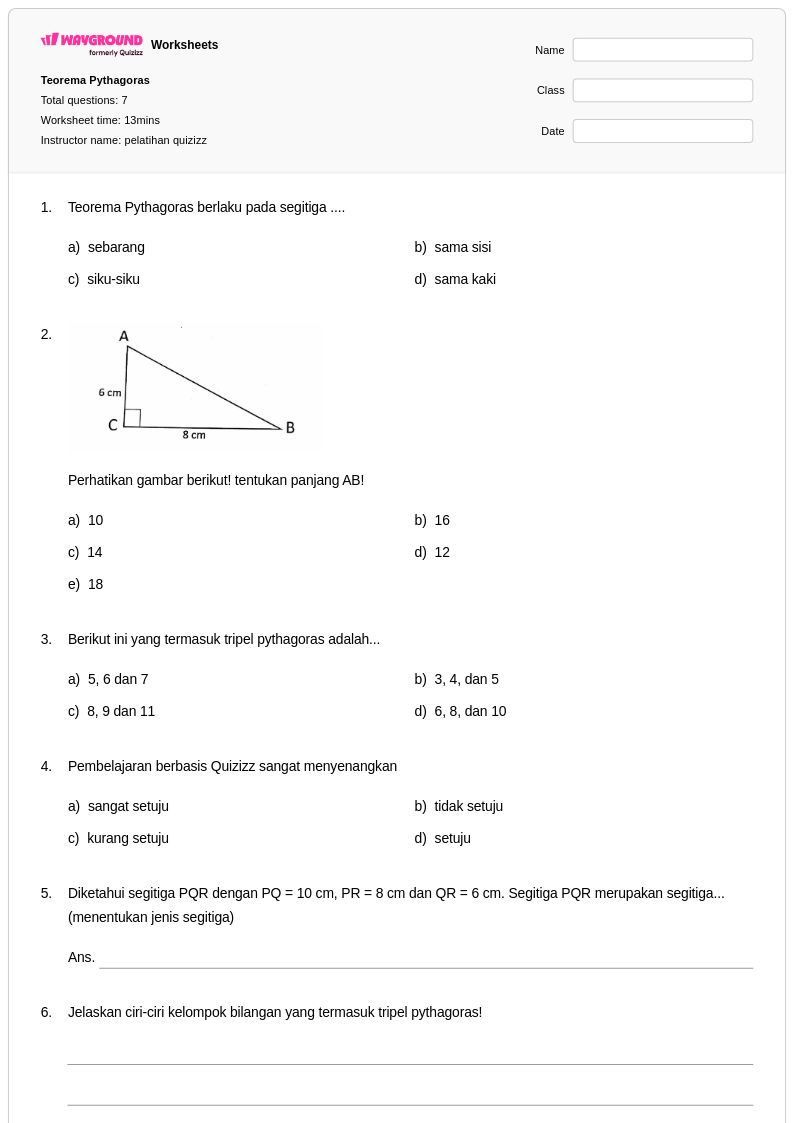
7Q
8th - Uni
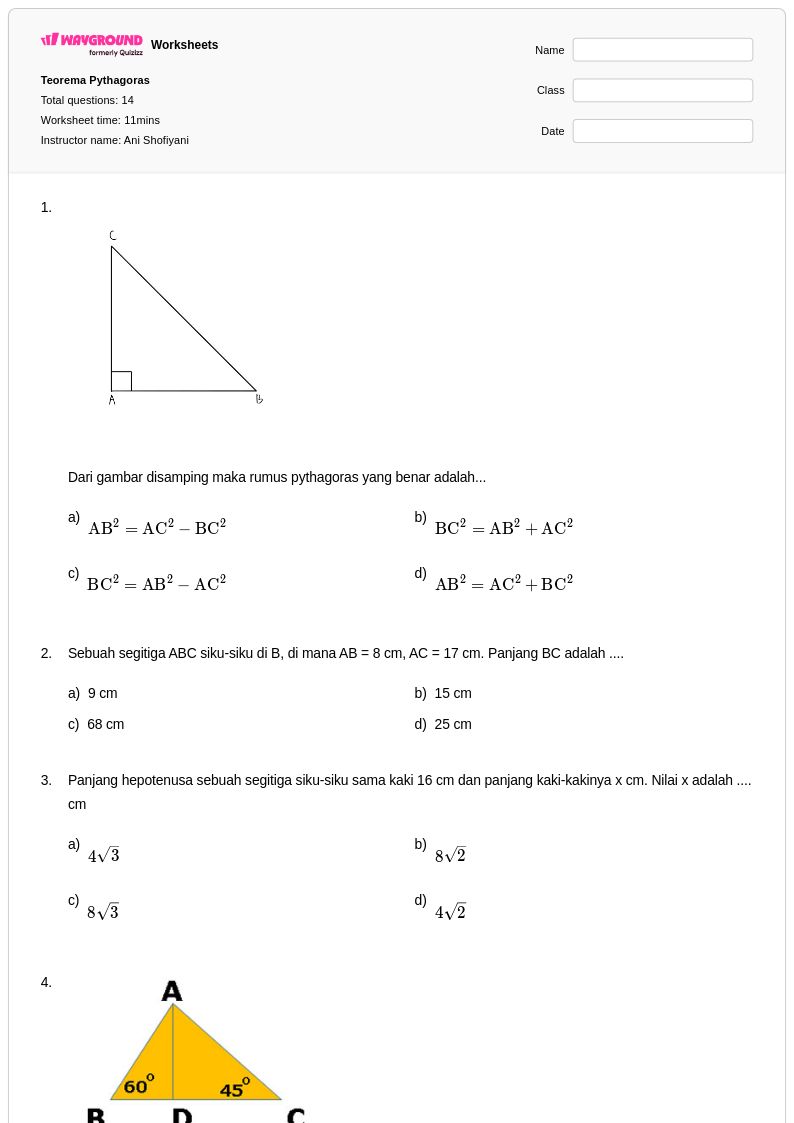
14Q
11th - 12th

15Q
11th
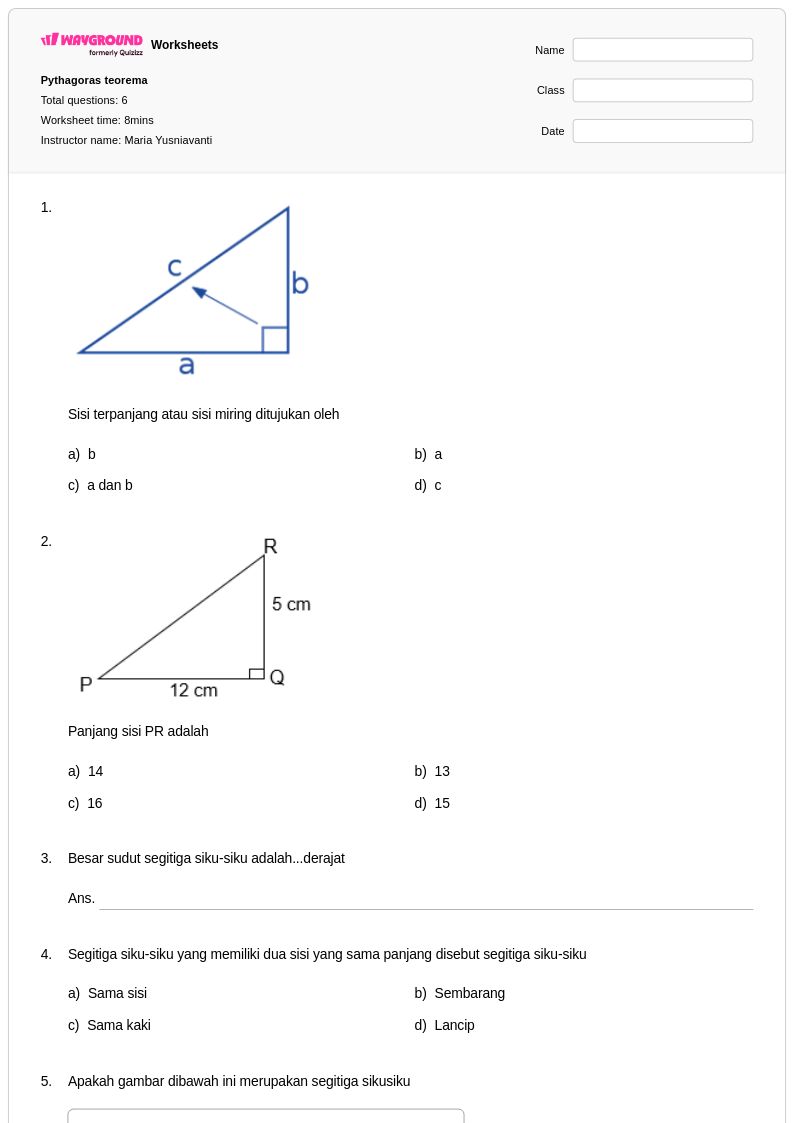
6Q
10th - 12th
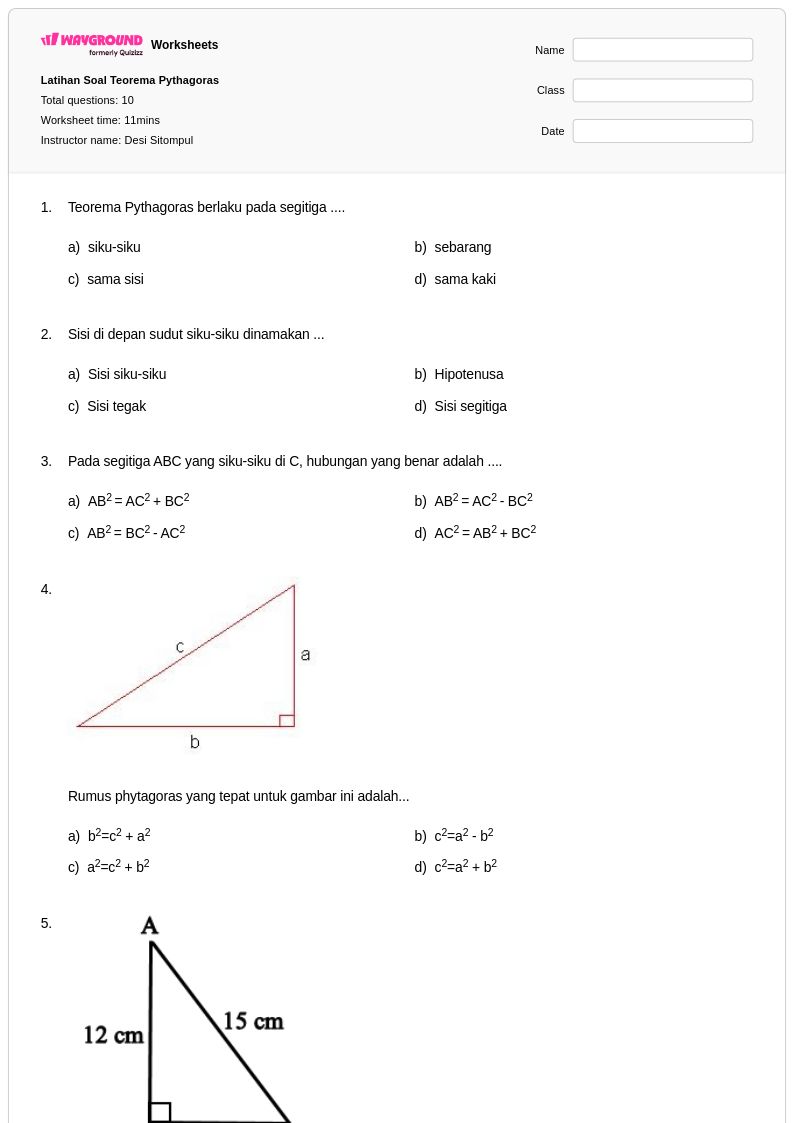
10Q
8th - Uni

10Q
11th

15Q
11th
20Q
8th - Uni

10Q
11th

8Q
11th

10Q
11th

10Q
11th

10Q
11th

5Q
9th - Uni

9Q
11th

10Q
11th
20Q
6th - 12th

10Q
11th

12Q
11th

25Q
11th

9Q
11th

10Q
11th
Explore otras hojas de trabajo de materias para kelas 11
Jelajahi lembar kerja Teorema Apit yang dapat dicetak untuk Kelas 11
Lembar kerja Teorema Apit untuk siswa kelas 11 yang tersedia melalui Wayground memberikan latihan komprehensif dengan salah satu teknik pencarian limit yang paling elegan dan ampuh dalam kalkulus. Sumber daya yang dirancang dengan cermat ini membantu siswa menguasai konsep fundamental penggunaan dua fungsi pembatas untuk menentukan limit fungsi ketiga yang terletak di antara keduanya, memperkuat keterampilan analitis kritis yang penting untuk studi kalkulus tingkat lanjut. Lembar kerja ini menampilkan soal latihan yang semakin menantang yang membimbing siswa dalam mengidentifikasi fungsi pembatas yang sesuai, menerapkan kondisi teorema, dan membuktikan keberadaan limit secara ketat. Setiap lembar kerja menyertakan kunci jawaban terperinci yang menunjukkan metode penyelesaian langkah demi langkah, menjadikan materi cetak gratis ini sangat berharga untuk pengajaran di kelas dan studi mandiri saat siswa mengembangkan kepercayaan diri dengan alat penalaran matematika yang canggih ini.
Koleksi sumber daya Teorema Apit yang luas yang dibuat oleh guru di Wayground menawarkan kepada pendidik matematika jutaan materi berkualitas tinggi dengan kemampuan pencarian dan penyaringan yang kuat yang memungkinkan identifikasi cepat konten yang sesuai untuk pengajaran kalkulus kelas 11. Lembar kerja yang selaras dengan standar platform ini mendukung pembelajaran diferensiasi melalui tingkat kesulitan yang dapat disesuaikan dan opsi format yang fleksibel, memungkinkan guru untuk menyesuaikan soal latihan untuk beragam kebutuhan siswa dan tujuan pembelajaran. Sumber daya komprehensif ini tersedia dalam format pdf yang dapat dicetak dan versi digital interaktif, memfasilitasi integrasi yang mulus ke dalam berbagai pendekatan pengajaran sekaligus mendukung perencanaan pelajaran yang efektif, remediasi yang ditargetkan untuk siswa yang kesulitan, dan peluang pengayaan bagi siswa tingkat lanjut yang mencari pemahaman lebih dalam tentang aplikasi teori limit.
