
13 คิว
10th - Uni
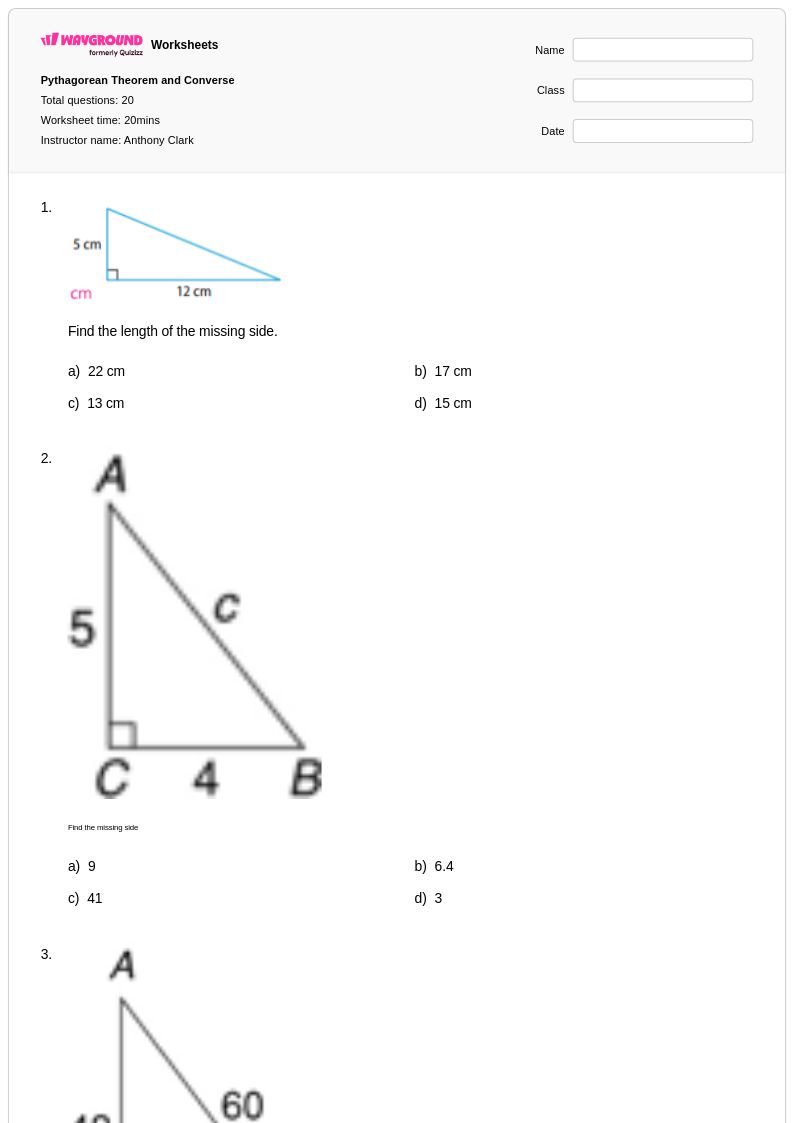
20 คิว
8th - Uni
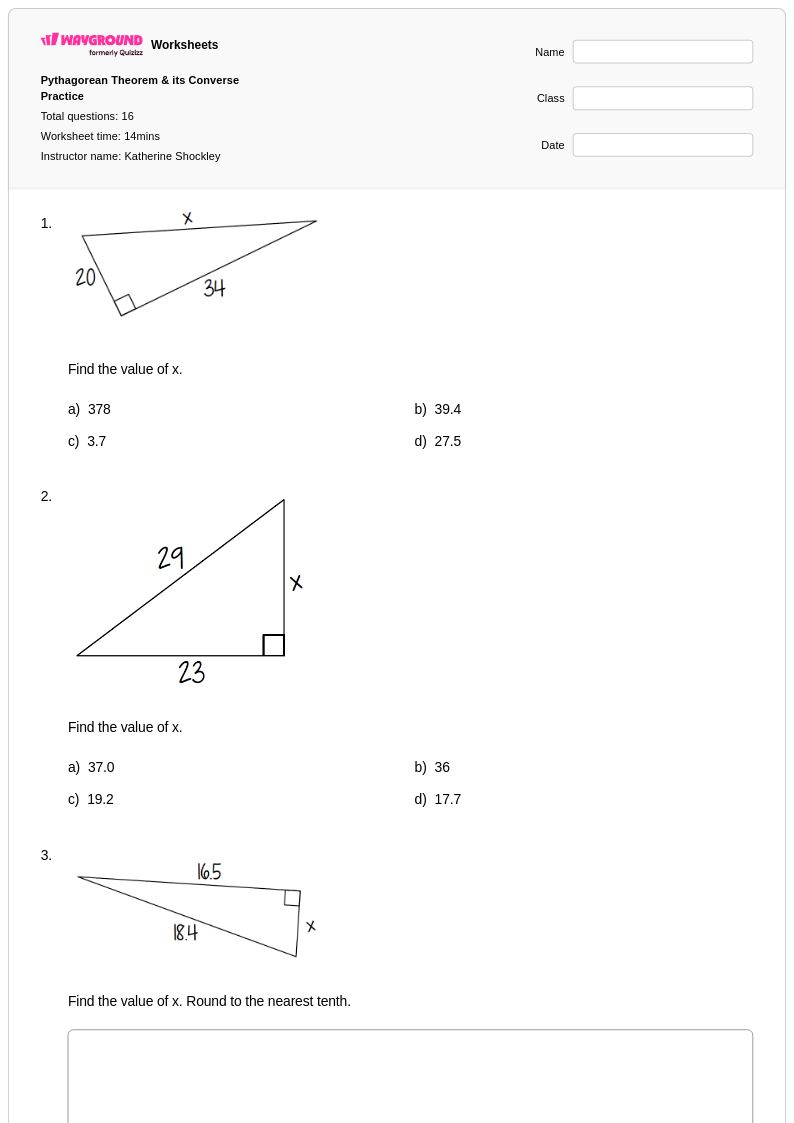
16 คิว
9th - 12th
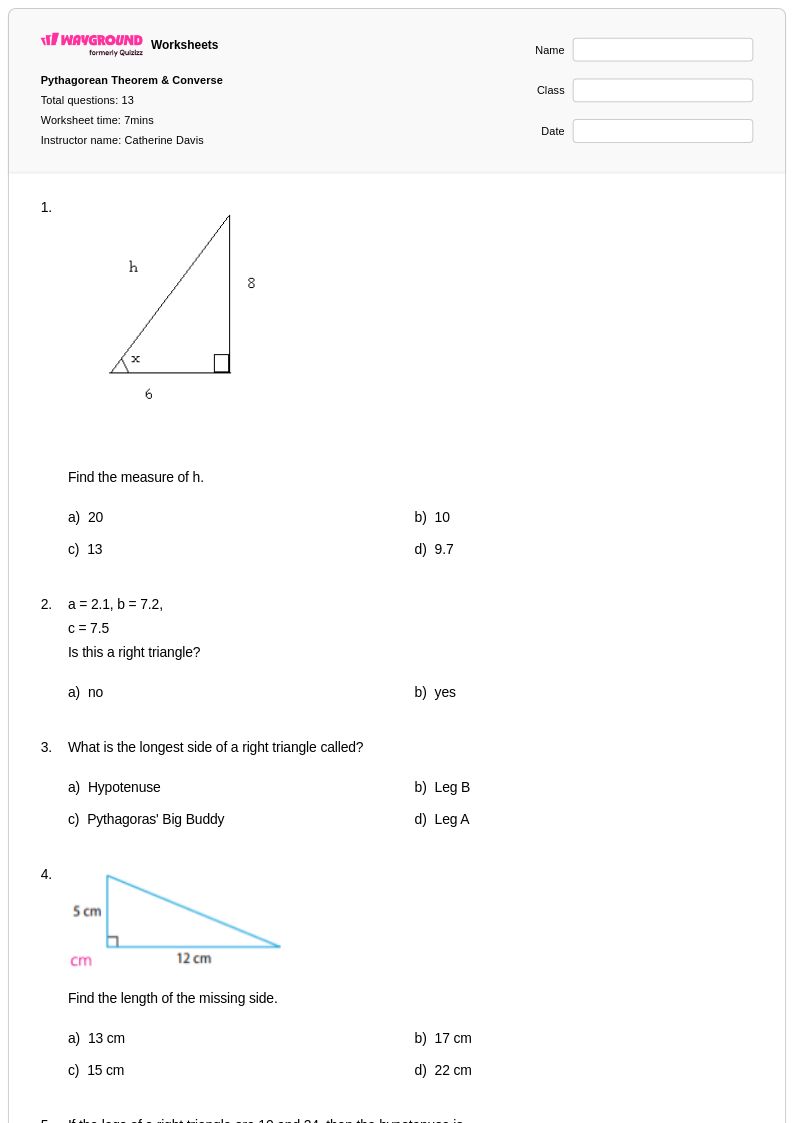
13 คิว
10th

20 คิว
9th - Uni

15 คิว
8th - 12th

21 คิว
9th - 12th
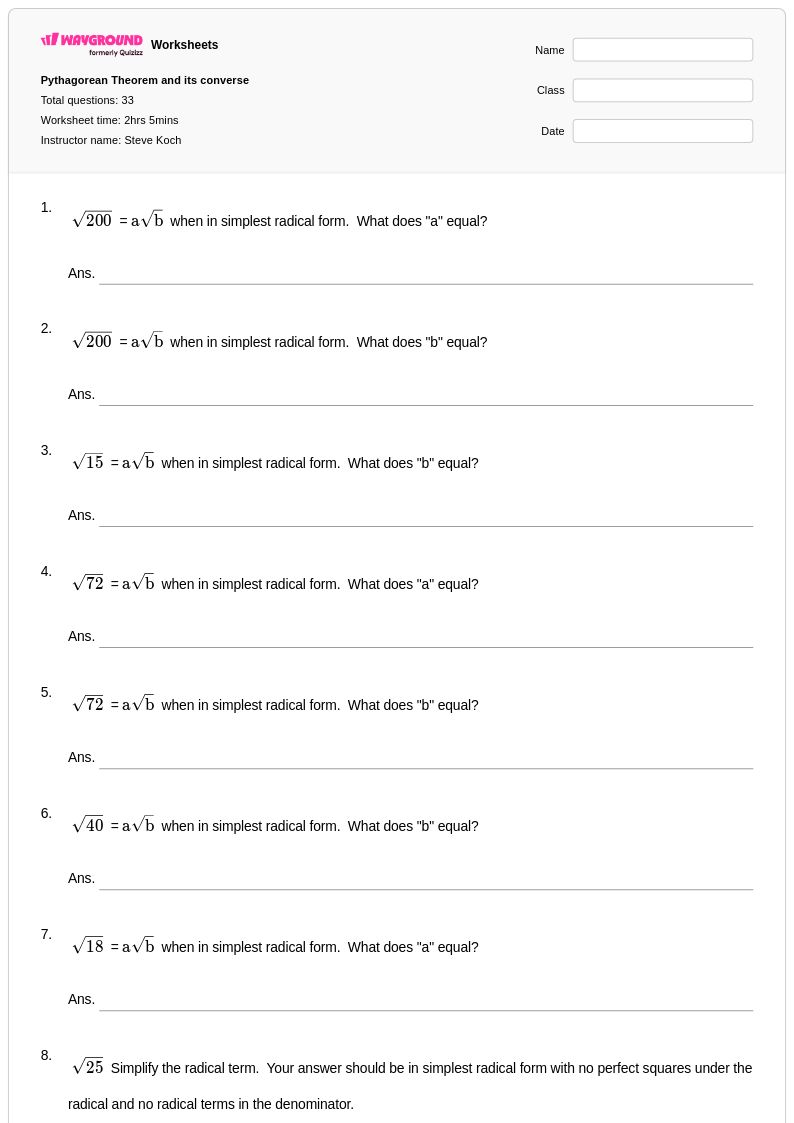
33 คิว
10th
16 คิว
10th

20 คิว
10th - Uni

20 คิว
8th - Uni
20 คิว
8th - Uni
13 คิว
10th
18 คิว
8th - Uni

25 คิว
10th
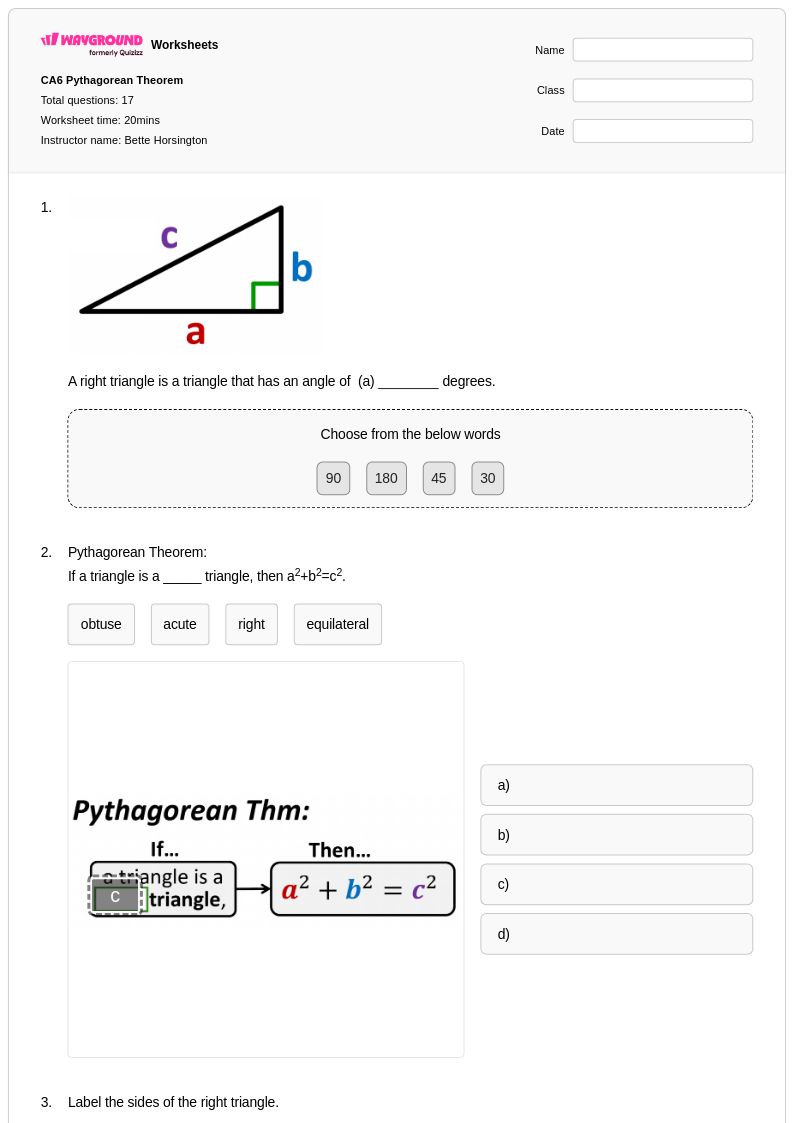
17 คิว
8th - Uni
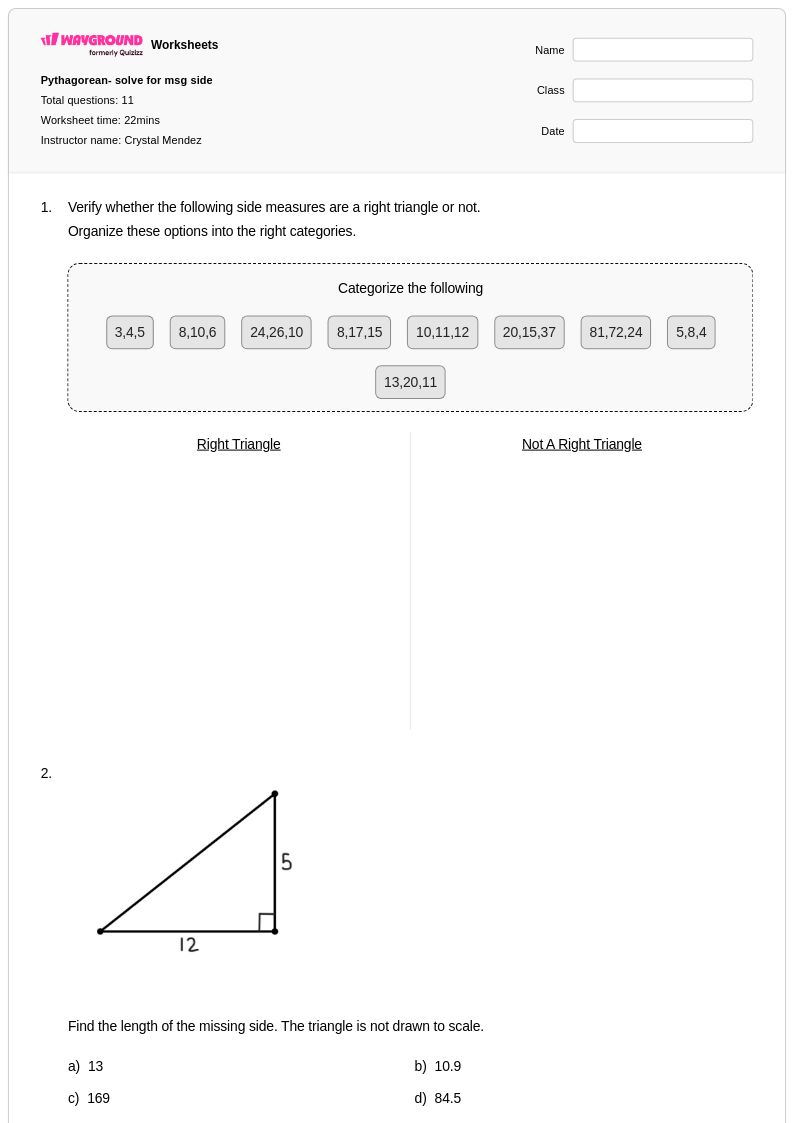
11 คิว
10th

19 คิว
8th - Uni

15 คิว
9th - 12th

18 คิว
9th - Uni

18 คิว
8th - Uni
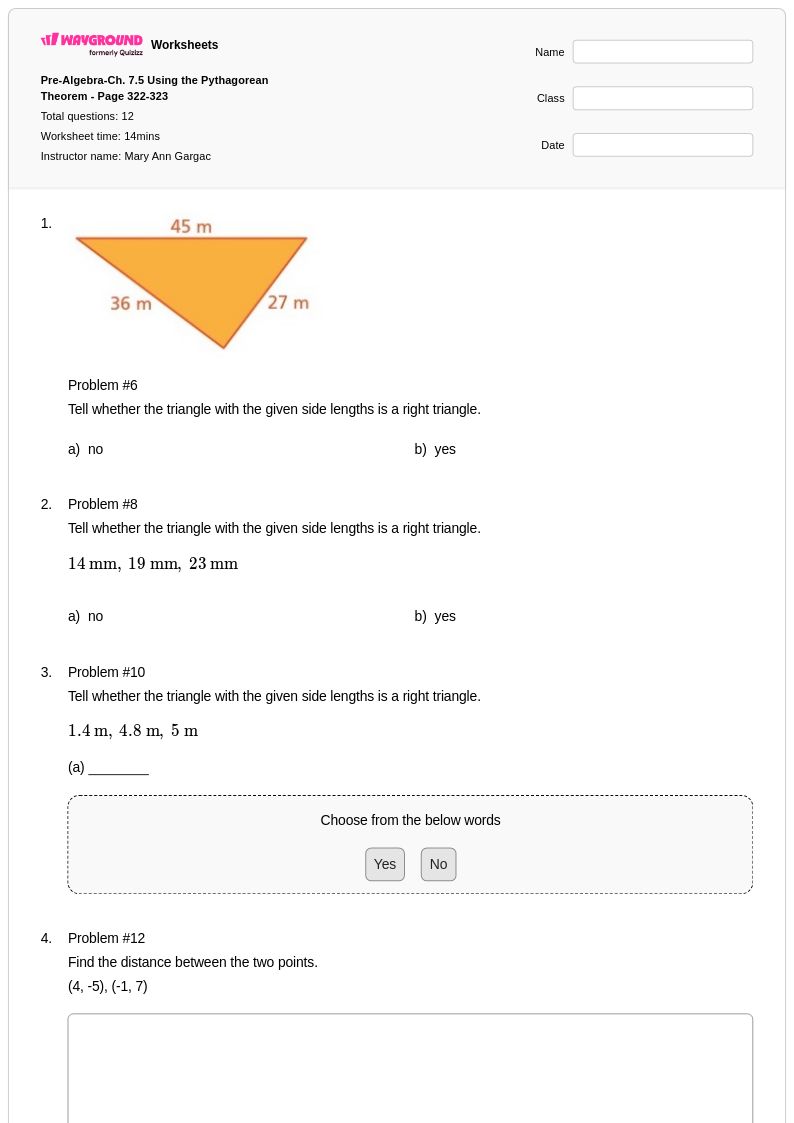
12 คิว
9th - 12th
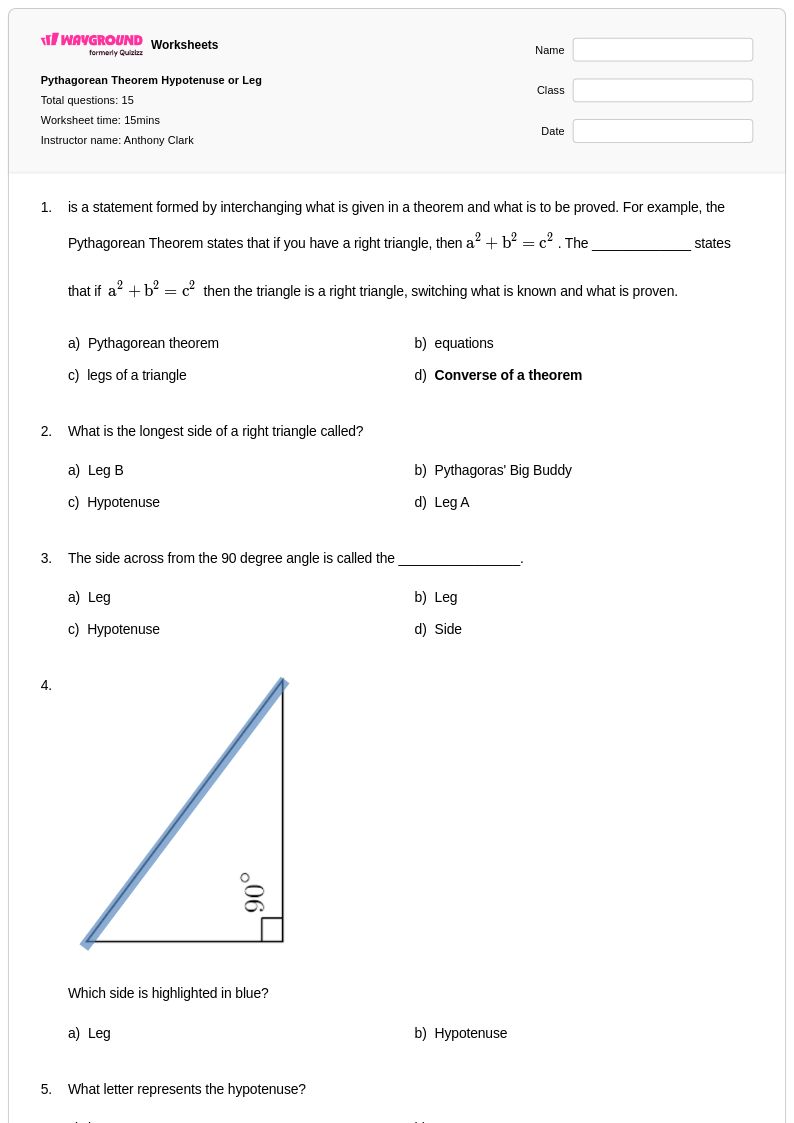
15 คิว
8th - Uni

5 คิว
9th - 12th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 10
สำรวจแผ่นงาน บทกลับของทฤษฎีบทพีทาโกรัส ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 10
แบบฝึกหัดทฤษฎีบทพีทาโกรัสผกผันจาก Wayground (เดิมคือ Quizizz) ช่วยให้นักเรียนชั้นมัธยมศึกษาปีที่ 4 ได้ฝึกฝนอย่างครอบคลุมในการพิจารณาว่าสามเหลี่ยมใดเป็นสามเหลี่ยมมุมฉากโดยพิจารณาจากความยาวด้าน แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างความเข้าใจของนักเรียนเกี่ยวกับการประยุกต์ใช้หลักการผกผันโดยการทดสอบว่ากำลังสองของด้านที่ยาวที่สุดเท่ากับผลรวมของกำลังสองของด้านอีกสองด้านหรือไม่ นักเรียนจะได้ฝึกฝนผ่านโจทย์ปัญหาอย่างเป็นระบบ ซึ่งจะช่วยสร้างความเชี่ยวชาญในการระบุสามเหลี่ยมมุมฉากจากขนาดที่กำหนด การวิเคราะห์การจำแนกประเภทของสามเหลี่ยม และการประยุกต์ใช้ทักษะการให้เหตุผลแบบผกผัน ซึ่งจำเป็นสำหรับการพิสูจน์ทางเรขาคณิตขั้นสูง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และสามารถดาวน์โหลดได้ฟรีในรูปแบบ PDF ที่สะดวก ช่วยให้นักเรียนสามารถตรวจสอบเหตุผลทางคณิตศาสตร์และพัฒนาความมั่นใจในแนวคิดตรีโกณมิติพื้นฐานนี้
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพครูผู้สอนด้วยแหล่งข้อมูลนับล้านรายการที่สร้างโดยนักการศึกษาโดยเฉพาะ ซึ่งมุ่งเน้นไปที่ทฤษฎีบทพีทาโกรัสผกผันและแนวคิดทางคณิตศาสตร์ที่เกี่ยวข้องสำหรับชั้นมัธยมศึกษาปีที่ 4 แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูผู้สอนสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรและตรงกับความต้องการเฉพาะของห้องเรียนได้อย่างรวดเร็ว เพื่อการสอนที่แตกต่างกัน ครูสามารถปรับแต่งสื่อที่มีอยู่หรือเข้าถึงชุดแบบฝึกหัดสำเร็จรูปที่มีให้ใช้งานทั้งในรูปแบบ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ ช่วยให้การวางแผนบทเรียนมีความยืดหยุ่นและสร้างสภาพแวดล้อมการเรียนรู้ที่หลากหลาย เครื่องมือที่ครอบคลุมเหล่านี้สนับสนุนการแก้ไขปัญหาอย่างมีประสิทธิภาพสำหรับนักเรียนที่ประสบปัญหา ให้โอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง และเสนอการฝึกฝนทักษะอย่างเป็นระบบที่ช่วยให้ครูติดตามความก้าวหน้าของนักเรียนในขณะที่สร้างความสามารถในการให้เหตุผลทางเรขาคณิตที่จำเป็น ซึ่งเป็นรากฐานสำหรับหลักสูตรคณิตศาสตร์ระดับสูงขึ้น
