
17 Hỏi
11th

7 Hỏi
7th

9 Hỏi
8th

10 Hỏi
8th

10 Hỏi
KG
8 Hỏi
Uni

50 Hỏi
Uni

166 Hỏi
Uni

15 Hỏi
KG

20 Hỏi
7th - 11th

47 Hỏi
10th

16 Hỏi
10th

8 Hỏi
Uni

10 Hỏi
Uni

20 Hỏi
1st

16 Hỏi
5th
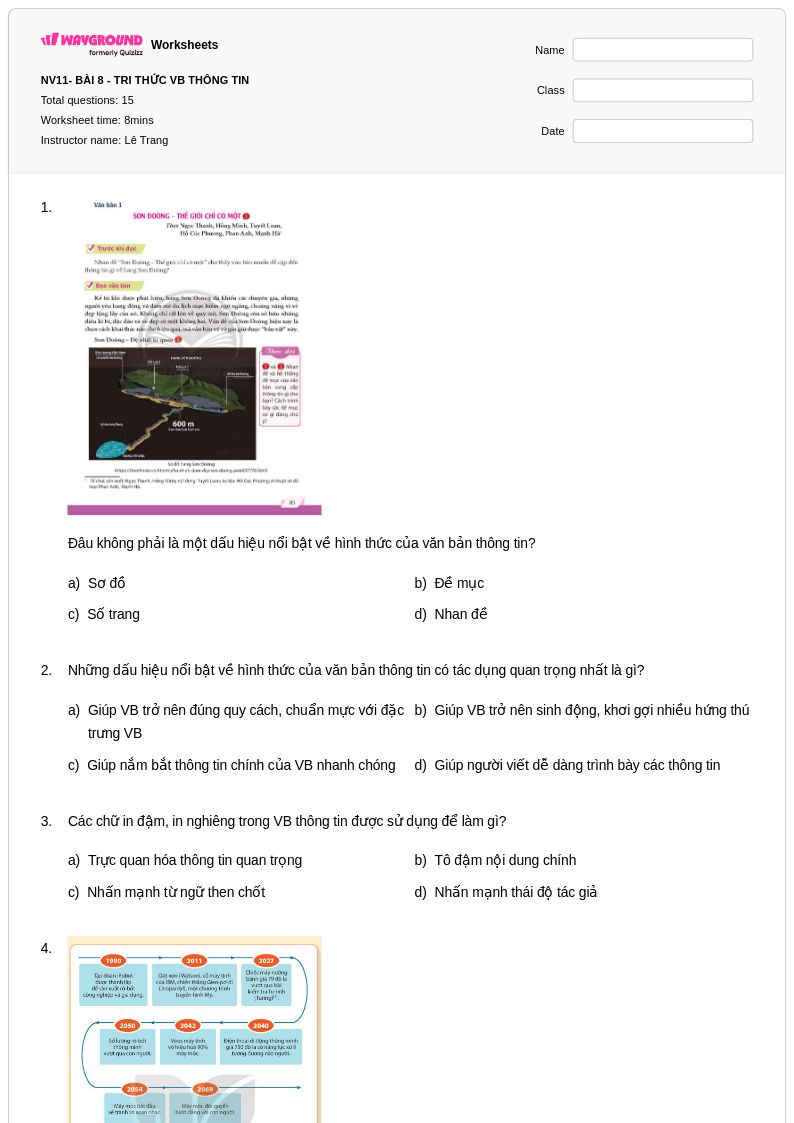
15 Hỏi
PD

18 Hỏi
Uni

22 Hỏi
PD

12 Hỏi
Uni

15 Hỏi
KG

15 Hỏi
KG

14 Hỏi
8th

15 Hỏi
Uni
Khám phá bảng tính theo chủ đề
Tương tác Hệ thống số Maya Bảng tính & câu đố
Các bài tập về hệ thống số Maya có sẵn trên Wayground (trước đây là Quizizz) cung cấp cho học sinh thực hành toàn diện để hiểu một trong những phát minh toán học tinh vi nhất trong lịch sử. Các tài nguyên giáo dục này tập trung vào hệ thống đếm nhị thập phân (cơ số 20) được phát triển bởi nền văn minh Maya, với sự kết hợp độc đáo giữa các dấu chấm, thanh ngang và ký hiệu vỏ sò để biểu thị các giá trị số. Học sinh tham gia vào các bài tập thực hành minh họa cách các nhà toán học Maya chỉ sử dụng ba ký hiệu—một dấu chấm cho số một, một thanh ngang cho số năm và một vỏ sò cho số không—để tạo ra các phép tính phức tạp và các quan sát thiên văn. Mỗi bộ bài tập bao gồm đáp án chi tiết và tài liệu giải thích, với các tài liệu in miễn phí có sẵn ở định dạng pdf để hỗ trợ cả việc giảng dạy trên lớp và tự học về hệ thống số đáng chú ý này.
Wayground (trước đây là Quizizz) hỗ trợ các nhà giáo dục với hàng triệu tài nguyên do giáo viên tạo ra, được thiết kế đặc biệt để khám phá các hệ thống toán học cổ đại như hệ thống số Maya. Khả năng tìm kiếm và lọc mạnh mẽ của nền tảng cho phép giáo viên nhanh chóng tìm thấy các tài liệu phù hợp với độ tuổi, phù hợp với các tiêu chuẩn về nghiên cứu xã hội và toán học, trong khi các công cụ phân hóa cho phép tùy chỉnh cho các nhu cầu học tập đa dạng. Các bộ bài tập này có cả phiên bản in và kỹ thuật số, bao gồm cả phiên bản PDF có thể tải xuống, rất lý tưởng cho việc lập kế hoạch bài học, ôn tập có mục tiêu và các hoạt động nâng cao kiến thức. Giáo viên có thể dễ dàng tích hợp các tài nguyên này vào các bài học về nền văn minh Maya, sử dụng các tùy chọn tùy chỉnh linh hoạt để tạo ra các buổi luyện tập kỹ năng hấp dẫn, giúp học sinh kết nối các khái niệm toán học cổ đại với sự hiểu biết về số học hiện đại.
