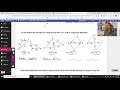
Triangle Congruence: SSS and SAS Postulates

What defines congruent triangles?

• They have the same size but different shapes.

• They have the same shape and size.

• They have the same shape but different sizes.

• They have different shapes and sizes.

Tags

CCSS.8.G.A.2

What is the Side-Side-Side (SSS) Congruence Postulate?

• If one pair of sides and two pairs of angles of one triangle are congruent to one pair of sides and two pairs of angles of another triangle, then the triangles are congruent.

• If three pairs of angles of one triangle are congruent to three pairs of angles of another triangle, then the triangles are congruent.

• If three pairs of sides of one triangle are congruent to three pairs of sides of another triangle, then the triangles are congruent.

• If two pairs of sides and one pair of angles of one triangle are congruent to two pairs of sides and one pair of angles of another triangle, then the triangles are congruent.

Tags

CCSS.HSG.SRT.B.5

In the SSS postulate, which pair of sides is congruent to side ZX?

• Side AC

• Side BC

• Side XY

• Side AB

Tags

CCSS.HSG.SRT.B.5

Which property allows side JL to be congruent to itself?

• Reflexive Property

• Associative Property

• Transitive Property

• Symmetric Property

Tags

CCSS.HSG.SRT.B.5

What additional information is needed to prove triangles congruent by SSS in the example with side RT?

• Angle T is congruent to angle Z

• Side RT is congruent to side XZ

• Side RT is congruent to side XY

• Angle R is congruent to angle X

Tags

CCSS.HSG.SRT.B.5

What is the Side-Angle-Side (SAS) Congruence Postulate?

• If one side and two angles of one triangle are congruent to one side and two angles of another triangle, then the triangles are congruent.

• If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.

• If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.

• If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.

Tags

CCSS.HSG.SRT.B.5

In the SAS postulate, which angle is the included angle between sides AB and BC?

• Angle D

• Angle A

• Angle B

• Angle C

Which postulate can be used to prove the triangles congruent if you have two sides and the included angle?

• SAS

• ASA

• AAS

• SSS

Tags

CCSS.HSG.SRT.B.5

What additional information is needed to use the SAS postulate in the example with angle L?

• Angle M is congruent to angle J

• Side LN is congruent to side HN

• Angle L is congruent to angle H

• Side LM is congruent to side HJ

What additional information is needed to use the SAS postulate in the example with vertical angles?

• Side DT is congruent to side ST

• Angle D is congruent to angle T

• Angle S is congruent to angle T

• Side DS is congruent to side TS