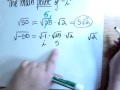
Simplifying Radicals with Imaginary Numbers

The video tutorial explains the concept of imaginary numbers, specifically the use of 'i' to handle negative numbers under a radical. It demonstrates how to simplify expressions involving 'i' and provides guidelines on where to place 'i' in mathematical expressions. The tutorial includes examples of simplifying square roots with and without negative numbers, emphasizing the correct placement of 'i' to avoid confusion.

What does 'i' represent in the context of complex numbers?

• A real number

• An operator

• The square root of -1

• A variable

Tags

CCSS.HSN.CN.A.1

What is the result of the square root of -25?

• 5

• -5i

• 5i

• -5

What is the square root of -1 commonly known as?

• Negative one

• Zero

• One

• i

Tags

CCSS.HSN.CN.A.1

What is the primary reason for using 'i' in complex numbers?

• To represent imaginary solutions

• To simplify expressions with negative radicals

• To denote indeterminate forms

• To add complexity

Tags

CCSS.HSN.CN.A.1

Where should 'i' be placed in the expression when simplifying square roots of negative numbers?

• After the radical

• Outside the expression

• Before the radical

• Under the radical

Tags

CCSS.HSN.CN.A.1

In expressions involving 'i', where should the number part be placed relative to 'i'?

• No specific order

• Below 'i'

• After 'i'

• Before 'i'

Tags

CCSS.HSN.CN.A.1

How do you simplify the square root of 50?

• 5√2

• √25 * √2

• 10

• 25√2

How is the square root of 50 simplified using the largest perfect square?

• 25√2

• 7.5

• √25 + √2

• 5√2

What is the simplified form of the square root of -32?

• 8i

• 16i

• 4√2

• 4i√2

What is the correct simplification of the square root of -32 using the largest perfect square?

• 4i√2

• 16i

• 8i

• 32i