Understanding Concavity and Points of Inflection

The video tutorial explains how to determine the intervals where a function is concave up or down and identify points of inflection. It begins with a review of concavity concepts, describing concave up as an upward-facing cup and concave down as a downward-facing cup. The tutorial uses algebraic methods to find average rates of change and illustrates these concepts with examples. It concludes by analyzing a graph to identify concave intervals and points of inflection, emphasizing the change in concavity at specific points.

What does it mean for a function to be concave up?

• The function's rate of change is decreasing.

• The function's rate of change is constant.

• The function's rate of change is increasing.

• The function has no rate of change.

Tags

CCSS.HSF-IF.C.7A

Which of the following best describes a concave up graph?

• A graph that looks like an upside-down cup.

• A graph that looks like a straight line.

• A graph that looks like an upward-facing cup.

• A graph that looks like a zigzag.

Tags

CCSS.HSF.LE.B.5

How can you determine if a function is concave down?

• The function has no points of inflection.

• The average rate of change is constant.

• The average rate of change is decreasing.

• The average rate of change is increasing.

Tags

CCSS.HSF-IF.C.7A

What shape does a concave down graph resemble?

• A zigzag pattern.

• An upside-down cup.

• A straight line.

• An upward-facing cup.

What is a point of inflection?

• A point where the function changes concavity.

• A point where the function is constant.

• A point where the function has no slope.

• A point where the function is undefined.

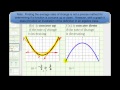
Where does the function change concavity in the given graph example?

• At the point (0,0).

• At the point (2,2).

• At the point (0,2).

• At the point (2,0).

In the graph example, what is the interval where the function is concave down?

• From negative infinity to 0.

• From 0 to positive infinity.

• From negative infinity to positive infinity.

• From 0 to 2.

In the graph example, what is the interval where the function is concave up?

• From negative infinity to 0.

• From negative infinity to positive infinity.

• From 0 to positive infinity.

• From 0 to 2.

Why is the point (0,2) considered a point of inflection in the graph example?

• Because it is where the function is undefined.

• Because it is where the function changes concavity.

• Because it is where the function has a maximum value.

• Because it is where the function has a minimum value.

What is the significance of not including 0 in the intervals of concavity?

• 0 is where the function is undefined.

• 0 is where the function has a minimum value.

• 0 is where the function has a maximum value.

• 0 is where the function changes concavity.