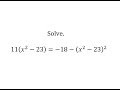
Solving Quadratic Equations and Functions

The video tutorial explains how to solve a quadratic equation by performing a substitution to simplify it into a basic quadratic form. The process involves setting the equation to zero, factoring it, and then substituting back to the original variable. The solutions are verified to ensure they satisfy the original equation, resulting in four possible solutions.

What is the first step in recognizing the given equation as a quadratic form?

• Solving for x

• Graphing the equation

• Factoring the equation

• Performing a substitution

Tags

CCSS.HSA-REI.B.4B

What substitution is made to simplify the equation into a basic quadratic form?

• u = x - 23

• u = x^2 + 23

• u = x + 23

• u = x^2 - 23

Tags

CCSS.HSA-REI.B.4B

After substitution, what is the next step to solve the quadratic equation?

• Set the equation equal to zero

• Graph the equation

• Add a constant to both sides

• Multiply both sides by a constant

Tags

CCSS.4.NBT.B.6

Which pair of numbers are the factors of 18 that add up to 11?

• 7 and 1

• 9 and 2

• 5 and 4

• 6 and 3

Tags

CCSS.HSA.APR.C.4

What is the result of substituting back the original variable into the factored equation?

• x^2 + 14 and x^2 + 21

• x^2 - 14 and x^2 - 21

• x^2 - 23 and x^2 - 9

• x^2 + 23 and x^2 + 9

Tags

CCSS.8.EE.A.2

What are the solutions for x when x^2 - 14 = 0?

• x = ±√23

• x = ±√14

• x = ±√9

• x = ±√21

Tags

CCSS.8.EE.A.2

What are the solutions for x when x^2 - 21 = 0?

• x = ±√23

• x = ±√9

• x = ±√21

• x = ±√14

Tags

CCSS.HSA-REI.B.4B

Why do we include a plus or minus sign when solving for x?

• To account for both positive and negative roots

• To simplify the equation

• To eliminate the variable

• To factor the equation

Tags

CCSS.HSA.REI.A.2

What is the purpose of verifying the solutions by substituting back into the original equation?

• To check if the solutions are correct

• To simplify the equation further

• To eliminate extraneous solutions

• To find new solutions

Tags

CCSS.HSA.REI.A.2

How many solutions are verified for the original equation?

• Two

• Three

• Five

• Four

Tags

CCSS.HSA.REI.A.2