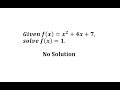
Understanding Quadratic Equations and Their Solutions

The video tutorial explains how to solve the equation f(x) = x^2 + 4x + 7 for f(x) = 1. It begins by substituting 1 for f(x) and simplifying the equation to x^2 + 4x + 6 = 0. The tutorial attempts to factor the equation but finds no real rational solutions, indicating the solutions are either irrational or complex. The video concludes with a graphical verification showing no intersection points, confirming the absence of real solutions.

What is the function f(x) that we are trying to solve for f(x) = 1?

• f(x) = x^2 + 4x + 7

• f(x) = x^2 + 3x + 5

• f(x) = x^2 + 5x + 6

• f(x) = x^2 + 2x + 4

Tags

CCSS.HSF.IF.A.2

What equation do we get after substituting 1 for f(x) in the function?

• x^2 + 2x + 4 = 0

• x^2 + 5x + 6 = 0

• x^2 + 3x + 5 = 0

• x^2 + 4x + 6 = 0

Tags

CCSS.HSA-REI.B.4B

Why can't the equation x^2 + 4x + 6 = 0 be factored using integers?

• The equation has no real solutions

• The equation is not quadratic

• The equation is already in its simplest form

• The sum of factors of 6 does not equal 4

Tags

CCSS.HSA-REI.B.4B

CCSS.HSN.CN.C.7

What does it mean when we say there are no real rational solutions to the equation?

• The equation has no solutions at all

• The solutions are imaginary

• The solutions are either irrational or complex

• The equation is incorrect

What does the graph of f(x) = x^2 + 4x + 7 and f(x) = 1 show about their solutions?

• The graphs overlap completely, indicating infinite solutions

• The graphs are parallel, indicating no solutions

• The graphs intersect at two points, indicating real solutions

• There are no points of intersection, indicating complex solutions