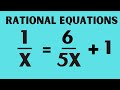
Rational Equations and Denominators
Interactive Video
•
Mathematics
•
7th - 10th Grade
•
Practice Problem
•
Hard
+3
Standards-aligned
Mia Campbell
FREE Resource
Standards-aligned
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the first step in solving a rational equation?
Cross-multiply the terms
Find the least common denominator
Add all terms to one side
Divide by the largest coefficient
Tags
CCSS.HSA.REI.A.2
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why can't we simply cross-multiply in the given rational equation?
Because it is not a valid method
Because the denominators are the same
Because the equation is not balanced
Because there is an extra term
Tags
CCSS.5.NF.A.1
CCSS.5.NF.A.2
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
After finding the least common denominator, what is the next step?
Subtract the denominators
Multiply each term by the LCM
Add the numerators
Divide each term by the LCM
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the result after simplifying the equation using the LCM?
A complex equation
A simple equation
An unsolvable equation
A quadratic equation
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the final step after simplifying the equation using the LCM?
Divide by the LCM again
Multiply by another factor
Solve the equation
Add more terms
Tags
CCSS.HSA.APR.D.7
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the complex denominator example, what is the chosen common denominator?
6x squared
6x
x squared
2x
Tags
CCSS.HSA.REI.A.2
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What happens when you multiply each term by the common denominator in the complex example?
The equation becomes more complex
The denominators remain unchanged
All fractions are eliminated
The equation becomes unsolvable
Tags
CCSS.HSA.REI.A.2
Create a free account and access millions of resources
Create resources
Host any resource
Get auto-graded reports

Continue with Google

Continue with Email

Continue with Classlink

Continue with Clever
or continue with

Microsoft
%20(1).png)
Apple
Others
Already have an account?
Popular Resources on Wayground

25 questions
Multiplication Facts
Quiz
•
5th Grade

15 questions
4:3 Model Multiplication of Decimals by Whole Numbers
Quiz
•
5th Grade

10 questions
The Best Christmas Pageant Ever Chapters 1 & 2
Quiz
•
4th Grade

12 questions
Unit 4 Review Day
Quiz
•
3rd Grade

20 questions
Christmas Trivia
Quiz
•
6th - 8th Grade

18 questions
Kids Christmas Trivia
Quiz
•
KG - 5th Grade

14 questions
Christmas Trivia
Quiz
•
5th Grade

15 questions
Solving Equations with Variables on Both Sides Review
Quiz
•
8th Grade
Discover more resources for Mathematics

15 questions
Solving Equations with Variables on Both Sides Review
Quiz
•
8th Grade

15 questions
scatter plots and trend lines
Quiz
•
8th Grade

20 questions
Slope from a Graph
Quiz
•
8th Grade

14 questions
8th U4L2 - Keeping Equations Balanced
Quiz
•
8th Grade

14 questions
finding slope from a graph
Quiz
•
8th Grade

20 questions
Scatter Plots and Line of Best Fit
Quiz
•
8th Grade

20 questions
One-Step Inequalities
Quiz
•
7th Grade

20 questions
Solving Proportions
Quiz
•
5th - 7th Grade