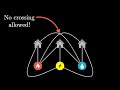
Topology and Graph Theory Concepts

The video features a group of YouTubers attempting to solve a classic puzzle involving connecting utilities to houses without crossing lines. The challenge is initially presented as impossible on a flat surface, leading to a discussion on graph theory and Euler's formula. The solution is revealed using a mug, exploiting its topological properties. The video concludes with insights into problem-solving and a mention of Brilliant.org for further learning.

What is the main challenge presented in the utilities puzzle?

• Maximizing the number of connections

• Minimizing the number of utilities

• Finding the shortest path between utilities

• Connecting utilities to houses without crossing lines

Why is the utilities puzzle considered impossible on a plane?

• Because there are too many utilities

• Due to the constraints of planar graphs

• Because the houses are too far apart

• Due to the lack of a proper drawing tool

What mathematical concept is used to prove the impossibility of the puzzle on a plane?

• Pascal's triangle

• Fibonacci sequence

• Euler's formula

• Pythagorean theorem

How does the mug's handle help in solving the puzzle?

• It acts as a bridge to prevent line crossings

• It provides extra space for drawing

• It changes the color of the lines

• It reduces the number of utilities

What is the topological shape of a mug that helps solve the puzzle?

• Cylinder

• Torus

• Cube

• Sphere

What is the significance of Euler's characteristic formula in the context of planar graphs?

• It determines the number of vertices and edges

• It remains constant for any planar graph

• It varies with the number of utilities

• It helps calculate the shortest path

What is the relationship between a mug and a donut in topology?

• They are both flat surfaces

• They are both considered spheres

• They are both topologically equivalent to a torus

• They are both used in Euler's formula

What is the benefit of using a dry erase marker on the mug?

• It makes the lines permanent

• It allows for easy correction of mistakes

• It changes the color of the mug

• It prevents the mug from being used

What is the main takeaway from the discussion on the mug's handle?

• It shows that the puzzle is unsolvable

• It proves the puzzle is easy

• It demonstrates a topological solution

• It suggests using a different puzzle

What is the purpose of introducing additional puzzles at the end?

• To provide more practice in problem-solving

• To confuse the viewers

• To introduce new mathematical concepts

• To show the complexity of the original puzzle