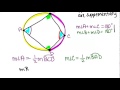
Inscribed Angles and Quadrilaterals

This video tutorial explains inscribed quadrilaterals in circles, focusing on their unique property where opposite angles are always supplementary. It delves into the concept of inscribed angles and their intercepted arcs, demonstrating how these angles relate to the circle's total 360 degrees. The tutorial uses equations to illustrate why the sum of opposite angles equals 180 degrees, providing a comprehensive understanding of the geometric principles involved.

What is an inscribed quadrilateral?

• A quadrilateral with all vertices inside the circle

• A quadrilateral with all vertices on the circle

• A quadrilateral with one vertex on the circle

• A quadrilateral with no vertices on the circle

What is the unique property of opposite angles in an inscribed quadrilateral?

• They are supplementary

• They are congruent

• They are complementary

• They are equal

Why do opposite angles in an inscribed quadrilateral add up to 180°?

• Because the quadrilateral is regular

• Due to the properties of inscribed angles and arcs

• Due to the properties of parallel lines

• Because the circle is symmetrical

What is the measure of a full circle in degrees?

• 180°

• 360°

• 270°

• 90°

How is the measure of an inscribed angle related to its intercepted arc?

• It is equal to the arc

• It is half the measure of the arc

• It is double the measure of the arc

• It is unrelated to the arc

What do the arcs BCD and BAD together form?

• A tangent

• The whole circle

• A quadrant

• A semicircle

What is the sum of all angles in any quadrilateral?

• 180°

• 270°

• 360°

• 90°

What is the result of dividing the sum of the measures of arcs BCD and BAD by two?

• 270°

• 180°

• 90°

• 360°

What is the relationship between the measure of angle A and arc BCD?

• Angle A is half of arc BCD

• Angle A is equal to arc BCD

• Angle A is unrelated to arc BCD

• Angle A is double arc BCD

What is the conclusion about opposite angles in an inscribed quadrilateral?

• They are always congruent

• They are always complementary

• They are always supplementary

• They are always equal