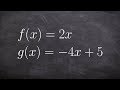
Understanding Division and Rational Functions

The video tutorial covers the basics of division, focusing on rational functions and their simplification. It explains the importance of constraints, particularly when dealing with division by zero. The concept of imaginary numbers is introduced, highlighting the need for a new set of numbers when dealing with negative square roots. The tutorial emphasizes the importance of identifying values that make the denominator zero and solving for constraints to avoid division by zero errors.

What is the basic operation being discussed in this section?

• Subtraction

• Division

• Addition

• Multiplication

Why can't the function 2x over negative 4x plus 5 be simplified further?

• Because it is a polynomial

• Because it involves imaginary numbers

• Because it is a complex number

• Because it is already in its simplest form

What type of number is 'i' in mathematics?

• Whole number

• Real number

• Imaginary number

• Rational number

Why can't we divide by zero?

• Because it results in a negative number

• Because it is undefined

• Because it is a rational number

• Because it results in a complex number

What is the result of multiplying zero by any number?

• Zero

• The original number

• One

• Infinity

What should be done to avoid division by zero in rational functions?

• Add a constant to the denominator

• Ignore the zero

• Multiply the numerator by zero

• Set the denominator equal to zero and solve for x

What is the constraint for the function 2x over negative 4x plus 5?

• x cannot equal 5

• x cannot equal 4

• x cannot equal 5/4

• x cannot equal 0

What happens if x equals 5/4 in the function 2x over negative 4x plus 5?

• The function becomes a complex number

• The numerator becomes zero

• The denominator becomes zero

• The function becomes undefined

What is the purpose of setting the denominator equal to zero in rational functions?

• To find the numerator

• To find the imaginary part

• To find the constraints

• To simplify the function

What is the main topic of this video tutorial?

• Rational functions and division

• Multiplication and division

• Addition and subtraction

• Complex numbers and division