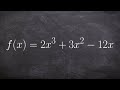
Analyzing Functions and Their Properties

The video tutorial explains how to determine if a function is even or odd by analyzing the function F(x) and its negative counterpart. It reviews the definitions of even and odd functions, discusses the symmetry of functions, and applies power rules to check the resultant function. Ultimately, it concludes that the given function is neither even nor odd.

What is the basic rule to identify an even function?

• F(x) = -F(-x)

• F(x) = F(x)

• F(x) = -F(x)

• F(x) = F(-x)

What is the basic rule to identify an odd function?

• F(x) = F(x)

• F(x) = -F(-x)

• F(x) = -F(x)

• F(x) = F(-x)

What is the original function F(x) discussed in the video?

• 2x^3 + 3x^2 - 12x

• 2x^2 + 3x^3 - 12x

• 3x^3 + 2x^2 - 12x

• 2x^3 - 3x^2 + 12x

What does the negative of the function F(x) look like?

• -2x^3 - 3x^2 + 12x

• 2x^3 + 3x^2 - 12x

• -2x^3 + 3x^2 - 12x

• 2x^3 - 3x^2 + 12x

What is the result when you plug in F(-x) for the given function?

• It looks like both

• It looks like the original function

• It looks like neither

• It looks like the negative of the original function

What happens when a negative number is raised to an odd power?

• It becomes undefined

• It becomes zero

• It remains negative

• It becomes positive

What happens when a negative number is raised to an even power?

• It remains negative

• It becomes zero

• It becomes positive

• It becomes undefined

What is the conclusion about the function F(x) = 2x^3 + 3x^2 - 12x?

• It is both even and odd

• It is odd

• It is even

• It is neither even nor odd