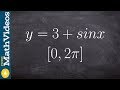
Concavity and Inflection Points

The video tutorial explains how to find intervals of concavity using the second derivative test. It begins with finding the first and second derivatives, then solving for when sine of x equals zero using the unit circle. The tutorial identifies points of inflection and checks points to determine changes in concavity. It concludes with a summary of the key concepts and emphasizes the importance of understanding the difference between points and values of inflection.

What is the primary test used to find intervals of concavity?

• First Derivative Test

• Second Derivative Test

• Limit Test

• Continuity Test

What is the first derivative of the function given in the video?

• sine of x

• cosine of x

• negative sine of x

• negative cosine of x

What is the second derivative of the function?

• negative cosine of x

• sine of x

• cosine of x

• negative sine of x

What equation do we solve to find potential inflection points?

• f(x) = 1

• f'(x) = 0

• f(x) = 0

• f''(x) = 0

At which values of x is sine of x equal to zero?

• x = 0, pi, 2pi

• x = pi/4, 3pi/4

• x = pi/3, 2pi/3

• x = pi/2, 3pi/2

Why are endpoints not included when identifying inflection points?

• Endpoints cannot have a change in concavity

• Endpoints are not part of the function

• Endpoints are always concave up

• Endpoints are always concave down

What is the possible point of inflection identified in the video?

• x = pi/2

• x = 0

• x = pi

• x = 2pi

What angle is chosen between 0 and pi to check concavity?

• pi/3

• pi/4

• pi/2

• 3pi/4

What is the sine value at 3pi/2?

• -1

• 0

• 1/2

• 1

What does a change from negative to positive in the second derivative indicate?

• Concave up to concave down

• Function is constant

• No change in concavity

• Concave down to concave up