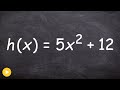
Inverse Functions and Operations

The video tutorial explains how to find the inverse of the function H(x) = 5x^2 + 12. The process involves replacing H(x) with y, swapping x and y, and using inverse operations to solve for y. The tutorial also covers taking the square root and applying constraints to ensure the inverse function is valid. The final inverse function is determined with a constraint that x must be greater than or equal to 12 to maintain a positive radicand.

What is the initial function given in the problem?

• H(x) = 5x + 12

• H(x) = 5x^2 + 12

• H(x) = 5x^3 + 12

• H(x) = 5x^2 - 12

What is the first step in finding the inverse of a function?

• Replace the function with y

• Solve for x

• Differentiate the function

• Swap x and y

Why do we replace H(x) with y?

• To avoid using x in the equation

• To change the function completely

• To simplify the algebraic process

• To make the function more complex

What is the next step after replacing H(x) with y?

• Integrate the function

• Differentiate the function

• Swap x and y

• Solve for x

What is the purpose of swapping x and y?

• To integrate the function

• To solve for y

• To solve for x

• To differentiate the function

What operation is used to undo subtraction in the equation?

• Exponentiation

• Division

• Multiplication

• Addition

After undoing multiplication by five, what is the resulting equation?

• x - 12 = y^2

• x + 12 = y^2

• x / 5 = y^2

• x - 12 / 5 = y^2

What is the purpose of taking the square root of both sides?

• To simplify the equation

• To eliminate the square

• To solve for y

• To solve for x

What is the inverse operation of squaring?

• Division

• Square root

• Multiplication

• Addition

Why is only the positive root considered for the inverse function?

• The negative root is invalid

• The positive root is simpler

• The negative root does not produce a function

• The positive root is more common