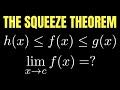
Limits and the Squeeze Theorem

The video tutorial introduces the squeeze theorem, also known as the pinching or sandwich theorem. It explains the conditions under which the theorem applies, involving inequalities and limits. Two examples are provided: one using the sine function and another using the cosine function, demonstrating how to apply the theorem to find limits as x approaches zero.

What is another name for the Squeeze Theorem?

• Compression Theorem

• Stretching Theorem

• Expansion Theorem

• Pinching Theorem

Which of the following is a condition for the Squeeze Theorem?

• The function must be squeezed between two others

• The function must be continuous

• The function must be periodic

• The function must be differentiable

In the first condition of the Squeeze Theorem, what is the relationship between h(x), f(x), and g(x)?

• h(x) > f(x) > g(x)

• h(x) < f(x) < g(x)

• h(x) ≤ f(x) ≤ g(x)

• h(x) = f(x) = g(x)

What must be true about the limits of h(x) and g(x) in the second condition of the Squeeze Theorem?

• They must both approach the same limit

• They must both be zero

• They must both approach infinity

• They must both be undefined

What happens to f(x) as x approaches c if it is squeezed between h(x) and g(x)?

• f(x) becomes undefined

• f(x) approaches the same limit as h(x) and g(x)

• f(x) approaches zero

• f(x) approaches infinity

What is the classic example used to illustrate the Squeeze Theorem?

• x^2 * cos(x)

• x * sin(1/x)

• x^2 * sin(x)

• x * cos(1/x)

What is the range of the sine function used in creating inequalities for Example 1?

• -π to π

• -2 to 2

• -1 to 1

• 0 to 1

What is the limit of -x as x approaches 0 in Example 1?

• 1

• 0

• -1

• Infinity

What is the final result of the limit of x * sin(1/x) as x approaches 0?

• 1

• 0

• Infinity

• -1

What is the function used in Example 2 to illustrate the Squeeze Theorem?

• x^3 * cos(2022/x^2021)

• x^2 * cos(2022/x^2021)

• x^2 * sin(2022/x^2021)

• x^3 * sin(2022/x^2021)