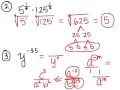
Exponents and Radicals Concepts

The video tutorial explains the process of converting radicals to rational exponents to simplify expressions. It covers examples of multiplying radicals, handling negative exponents, and rationalizing denominators. The tutorial emphasizes the importance of understanding the rules of exponents and provides step-by-step examples to illustrate these concepts.

Why might it be beneficial to convert a radical to a rational exponent?

• It makes the expression more complex.

• It allows for easier multiplication of terms.

• It eliminates the need for a calculator.

• It changes the base of the expression.

What is the rule for adding exponents when the bases are the same?

• Multiply the exponents.

• Subtract the exponents.

• Add the exponents.

• Divide the exponents.

How can you simplify the expression x^(1/2) back into a radical?

• x^(1/2) is already simplified.

• Rewrite it as the square root of x.

• Convert it to x^2.

• Leave it as x^(1/2).

When multiplying radicals with the same index, what is the first step?

• Divide the radicands.

• Subtract the radicands.

• Multiply the radicands.

• Add the radicands.

What is the result of multiplying 5 and 125 under a fourth root?

• 125

• 25

• 625

• 5

How do you handle a negative exponent in an expression?

• Ignore the negative sign.

• Move the base to the opposite side of the fraction.

• Multiply the base by -1.

• Add 1 to the exponent.

What is the equivalent fraction of the decimal 3.5?

• 5/2

• 3/2

• 7/3

• 7/2

What is the purpose of rationalizing the denominator?

• To change the base of the expression.

• To eliminate radicals from the denominator.

• To add more radicals to the expression.

• To make the expression more complex.

How do you rationalize a denominator with a square root?

• Multiply by the square root of the numerator.

• Multiply by the square root of the denominator.

• Add the square root to the numerator.

• Subtract the square root from the denominator.