Understanding Parallelograms and Area

The video tutorial explains how to find the area of a parallelogram by comparing it to a rectangle. It highlights the importance of identifying the correct height in a parallelogram, which differs from a rectangle due to the absence of right angles. The tutorial provides a step-by-step guide to calculating the area using the formula base times height, emphasizing the need to measure the perpendicular distance from the base to the top. The example used involves a parallelogram with a base of 7.4 feet and a height of 2 feet, resulting in an area of 14.8 square feet.

What is a key characteristic of a parallelogram that makes it similar to a rectangle?

• It has all sides of equal length.

• It has two sets of parallel sides.

• It has equal diagonals.

• It has four right angles.

Which formula is used to calculate the area of a rectangle?

• Area = base + height

• Area = base / height

• Area = base x height

• Area = base - height

When converting a rectangle to a parallelogram, what happens to the 90° angles?

• They are no longer present.

• They become obtuse angles.

• They remain unchanged.

• They become acute angles.

Why is it important to identify the correct height in a parallelogram?

• Because it determines the length of the base.

• Because it is equal to the base.

• Because it changes the shape of the parallelogram.

• Because it affects the calculation of the area.

How does the height of a parallelogram change as the shape is altered?

• It becomes longer.

• It remains the same.

• It becomes shorter.

• It becomes wider.

What is the correct way to measure the height of a parallelogram?

• From the base to the top, perpendicular to the base.

• From one side to the opposite side.

• From one corner to the opposite corner.

• Along the slanted side.

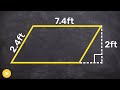
In the example given, what is the base length of the parallelogram?

• 3.7 feet

• 2 feet

• 7.4 feet

• 14.8 feet

What is the height used in the final calculation of the parallelogram's area?

• 2.4 feet

• 3 feet

• 7.4 feet

• 2 feet

What is the area of the parallelogram calculated in the example?

• 16 square feet

• 10 square feet

• 14.8 square feet

• 12 square feet

Why is the length of the slanted side not used as the height in a parallelogram?

• Because it is longer than the base.

• Because it is shorter than the base.

• Because it is not perpendicular to the base.

• Because it is equal to the base.