Graphing Circles and Inequalities

The video tutorial explains how to graph the inequality x^2 + y^2 ≥ 16 by recognizing it as a circle. The center of the circle is determined to be at the origin (0,0) with a radius of 4. The tutorial guides viewers through plotting the circle on a graph, emphasizing the importance of using a solid line for the circle due to the 'greater than or equal to' condition. Finally, it explains how to determine the correct region to shade, which is outside the circle, by testing a point within the circle and finding the inequality false.

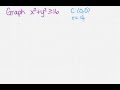
What type of geometric shape does the inequality x^2 + y^2 ≥ 16 represent?

• A square

• A triangle

• A circle

• A rectangle

What is the center of the circle represented by the equation x^2 + y^2 = 16?

• (16, 16)

• (1, 1)

• (4, 4)

• (0, 0)

How do you determine the radius of the circle from the equation x^2 + y^2 = 16?

• By taking the square root of 16

• By doubling 16

• By adding 16 to itself

• By halving 16

What is the radius of the circle represented by the equation x^2 + y^2 = 16?

• 2

• 16

• 4

• 8

When plotting the circle, how many units do you move from the origin to mark the radius?

• 4 units

• 2 units

• 5 units

• 3 units

What does the 'greater than or equal to' sign in the inequality indicate about the circle's boundary?

• It should be a double line

• It should be a dotted line

• It should be a solid line

• It should be a dashed line

If the inequality was x^2 + y^2 > 16, how would the circle's boundary be represented?

• As a dotted line

• As a double line

• As a solid line

• As a dashed line

Why is the circle in the graph solid?

• Because the center is at the origin

• Because the inequality includes equality

• Because the inequality is strict

• Because the radius is large

Which point is tested to decide where to shade on the graph?

• (4, 4)

• (2, 2)

• (1, 1)

• (0, 0)

What conclusion is drawn from testing the point (0, 0) in the inequality x^2 + y^2 ≥ 16?

• The point is on the boundary

• The point satisfies the inequality

• The point is outside the circle

• The point does not satisfy the inequality