
13Q
4th

7Q
2nd
20Q
1st - Uni

13Q
5th

7Q
4th

15Q
4th
8Q
7th
5Q
7th

20Q
5th

5Q
8th

6Q
1st - 3rd
6Q
3rd

18Q
4th
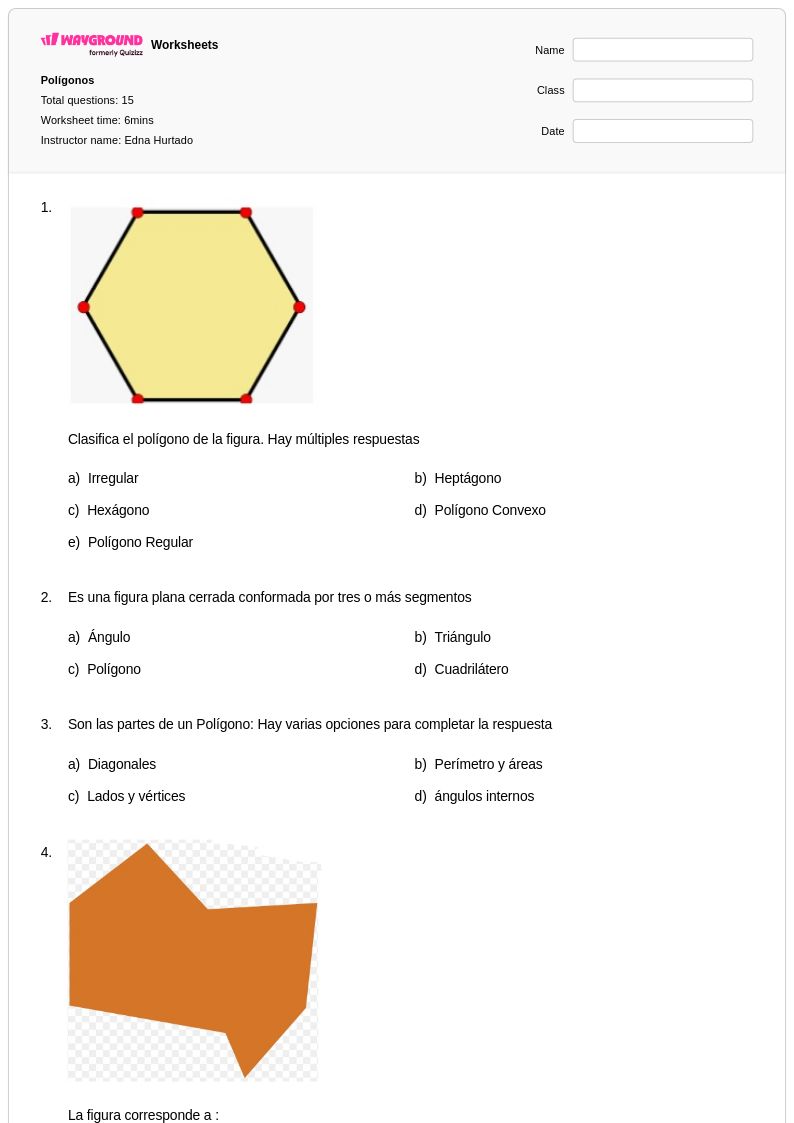
15Q
6th

13Q
4th

7Q
5th

10Q
7th

15Q
6th
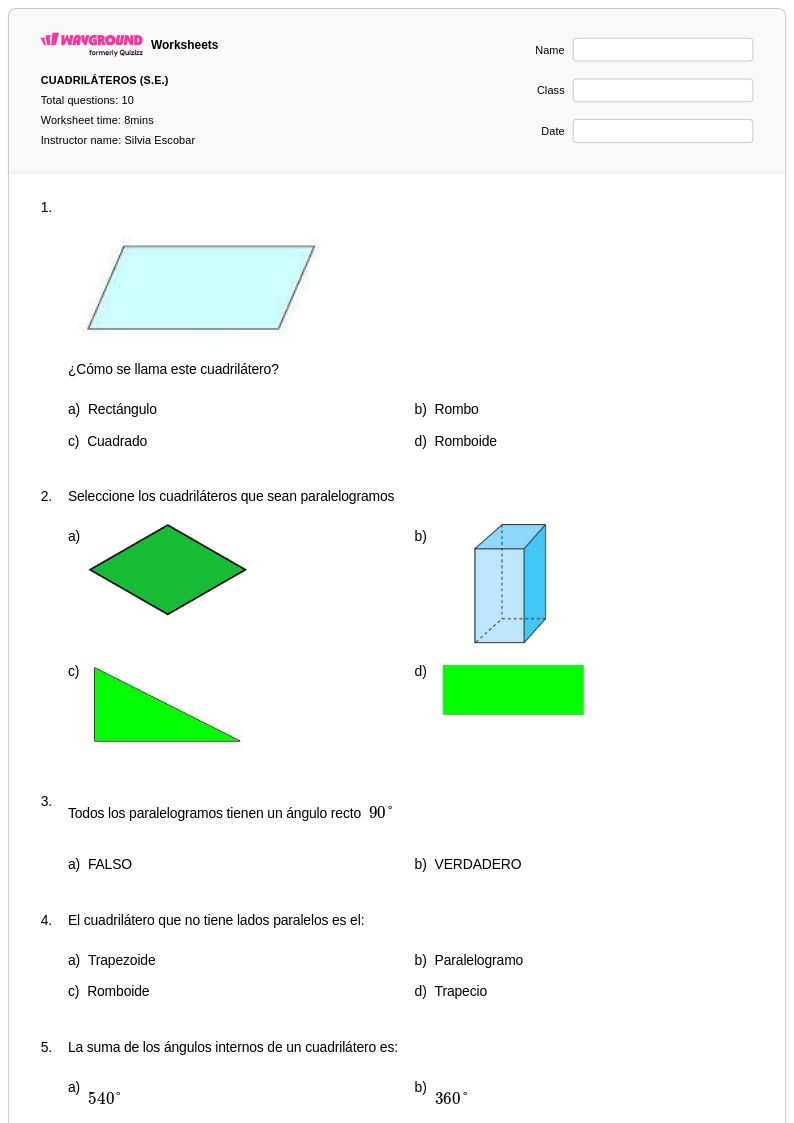
10Q
8th

10Q
2nd

23Q
5th

20Q
7th

15Q
5th

20Q
4th
Explorar hojas de trabajo por materias
Explore las hojas de trabajo imprimibles de Trapecios
Las hojas de ejercicios de trapecios, disponibles en Wayground (anteriormente Quizizz), ofrecen oportunidades prácticas integrales para que los estudiantes dominen las propiedades y los cálculos asociados con estos singulares cuadriláteros. Estos recursos, cuidadosamente diseñados, fortalecen habilidades geométricas esenciales, como la identificación de las características de los trapecios, el cálculo del área y el perímetro, la búsqueda de ángulos faltantes y la comprensión de las relaciones entre bases paralelas y catetos. Los estudiantes resuelven diversos ejercicios de práctica que refuerzan conceptos como trapecios isósceles, cálculos de medianas y aplicaciones de geometría de coordenadas con trapecios. Cada colección de hojas de ejercicios incluye claves de respuestas detalladas para apoyar el aprendizaje independiente y la autoevaluación, con imprimibles gratuitos disponibles en práctico formato PDF tanto para la enseñanza en clase como para las tareas.
Wayground (anteriormente Quizizz) brinda a los educadores acceso a millones de hojas de ejercicios de trapecios creadas por profesores que agilizan la planificación de las clases y la enseñanza diferenciada. Las robustas funciones de búsqueda y filtrado de la plataforma permiten a los profesores encontrar rápidamente recursos adaptados a los estándares de aprendizaje específicos y a los niveles de habilidad de los estudiantes, mientras que las herramientas de personalización permiten a los educadores modificar las hojas de ejercicios existentes o crear conjuntos de ejercicios específicos para la corrección y el enriquecimiento. Estos recursos de trapecio están disponibles en formato imprimible y digital, incluyendo archivos PDF descargables, lo que los hace ideales para diversos entornos de aprendizaje y escenarios de enseñanza. Los profesores pueden abordar eficazmente las diversas necesidades de los estudiantes seleccionando desde ejercicios básicos de identificación de propiedades hasta actividades avanzadas de resolución de problemas, garantizando así que cada alumno reciba la práctica adecuada de sus habilidades y el apoyo matemático necesario.
