
15 P
8th

15 P
3rd
8 P
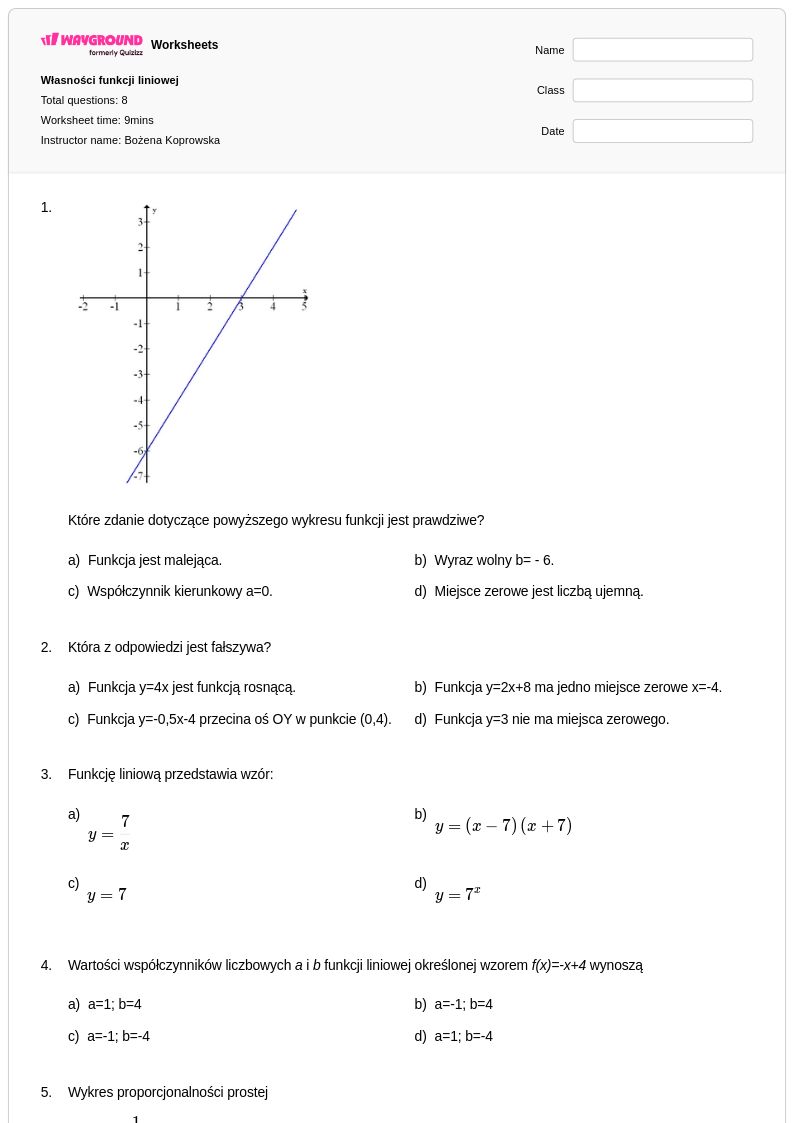
3rd
19 P
1st

10 P
8th

14 P
1st - 6th
10 P
6th
19 P
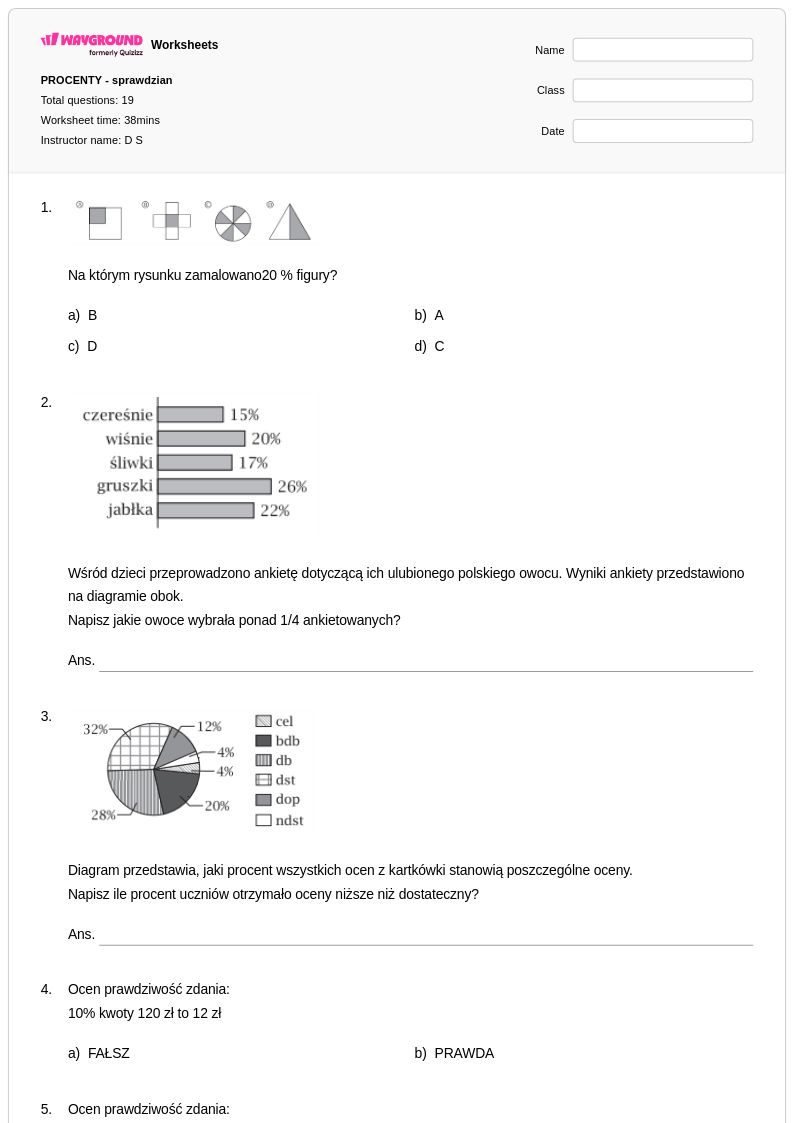
6th

16 P
2nd

8 P
6th

6 P
KG

20 P
4th

16 P
2nd

6 P
8th

10 P
4th - 9th

18 P
7th - 8th
9 P
KG - 5th

14 P
5th

5 P
8th

12 P
6th

15 P
9th - 12th

35 P
8th

16 P
6th
10 P
1st - 6th
Przeglądaj arkusze według tematów
Przeglądaj arkusze robocze Fakty dotyczące podziału do wydrukowania
Arkusze ćwiczeń z dzielenia dostępne w Wayground (dawniej Quizizz) zapewniają uczniom kompleksowe możliwości praktycznego opanowania podstawowych umiejętności dzielenia i osiągnięcia biegłości obliczeniowej. Te starannie zaprojektowane materiały do druku koncentrują się na pomocy uczniom w zapamiętywaniu podstawowych faktów z dzielenia, jednocześnie budując pewność siebie dzięki systematycznym zadaniom praktycznym, które wzmacniają związek między mnożeniem a dzieleniem. Każdy zbiór arkuszy ćwiczeń zawiera klucze odpowiedzi, które wspierają samodzielną naukę i samoocenę, a format PDF zapewnia łatwą dystrybucję i spójne formatowanie na różnych urządzeniach. Bezpłatne zasoby kładą nacisk na szybkie przypomnienie sobie faktów z dzielenia, co stanowi podstawę bardziej złożonych pojęć matematycznych, takich jak dzielenie pisemne, działania na ułamkach i myślenie algebraiczne.
Wayground (dawniej Quizizz) oferuje nauczycielom miliony stworzonych przez nich zasobów z faktami z dzielenia, które usprawniają planowanie lekcji i różnicują nauczanie, aby sprostać zróżnicowanym potrzebom uczniów. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć arkusze ćwiczeń dostosowane do określonych standardów i poziomów umiejętności, a narzędzia do personalizacji umożliwiają nauczycielom modyfikację treści w celu ukierunkowanych działań naprawczych lub wzbogacających. Te obszerne zbiory są dostępne zarówno w formacie do druku, jak i cyfrowym, w tym w plikach PDF do pobrania, które wspierają elastyczne wdrażanie nauczania, niezależnie od tego, czy uczniowie uczą się stacjonarnie, czy zdalnie. Nauczyciele mogą sprawnie śledzić postępy uczniów i identyfikować obszary wymagające dodatkowej praktyki, co czyni te zasoby nieocenionymi w budowaniu biegłości matematycznej poprzez systematyczny rozwój umiejętności i strategiczną interwencję.
