
25 Hỏi
10th - 12th

14 Hỏi
12th

10 Hỏi
9th - Uni

21 Hỏi
9th - 12th

6 Hỏi
3rd - Uni
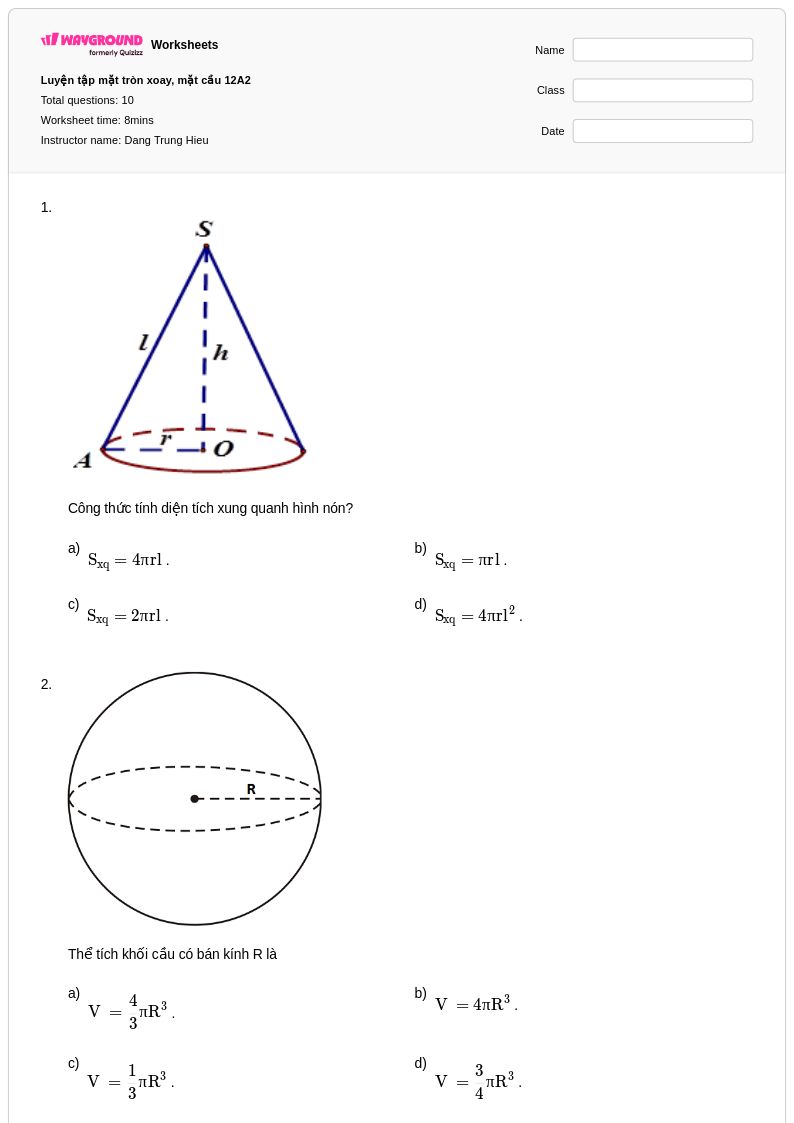
10 Hỏi
9th - 12th

10 Hỏi
9th - 12th
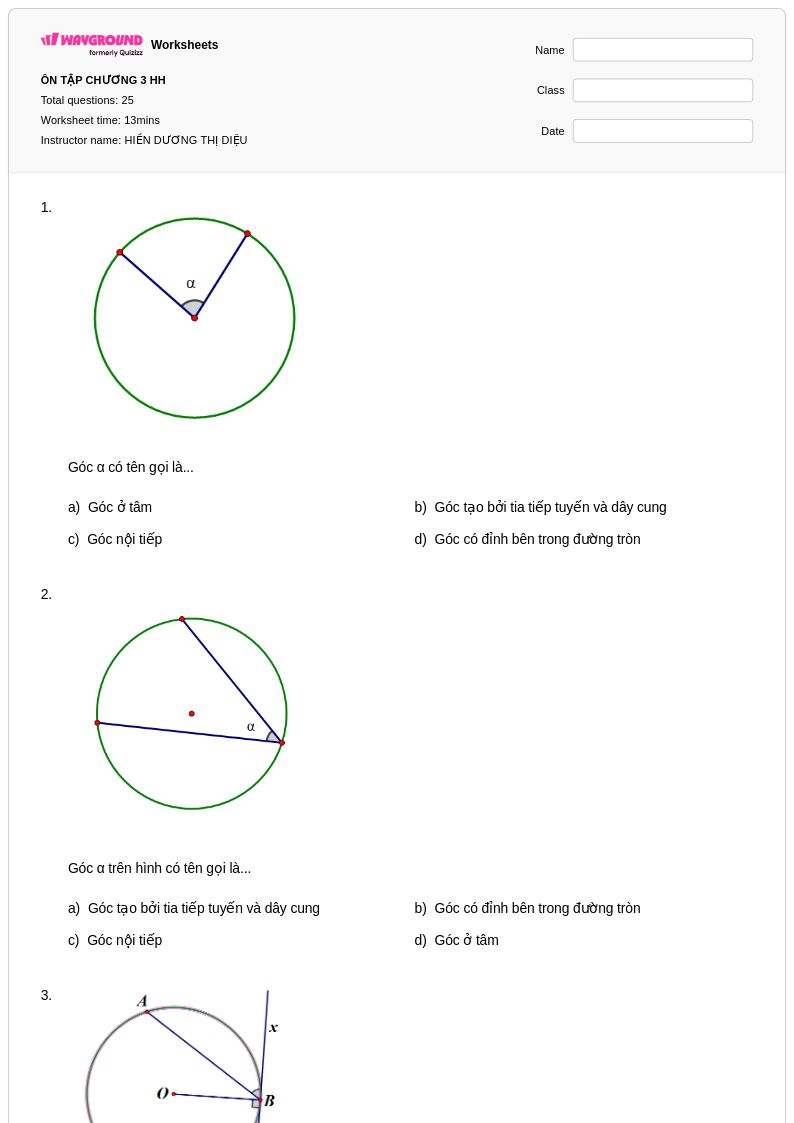
25 Hỏi
9th - 12th

10 Hỏi
9th - Uni

18 Hỏi
12th
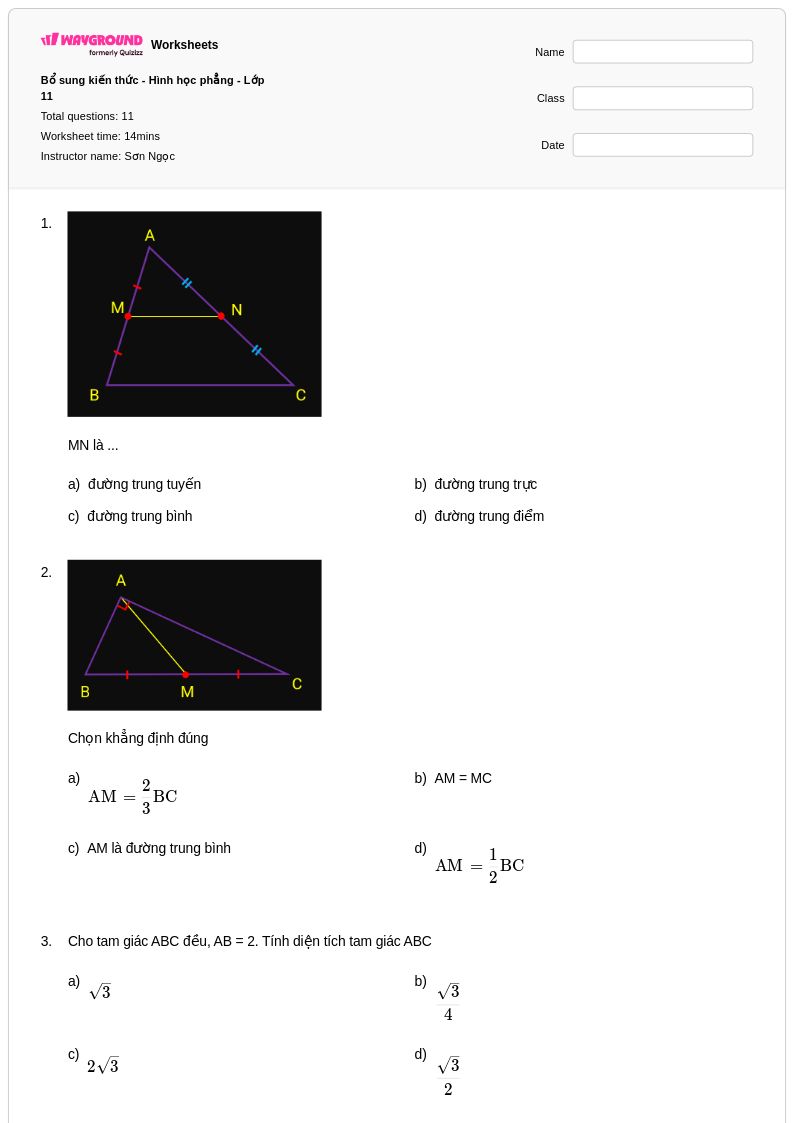
11 Hỏi
9th - 12th

10 Hỏi
12th

10 Hỏi
12th

10 Hỏi
12th
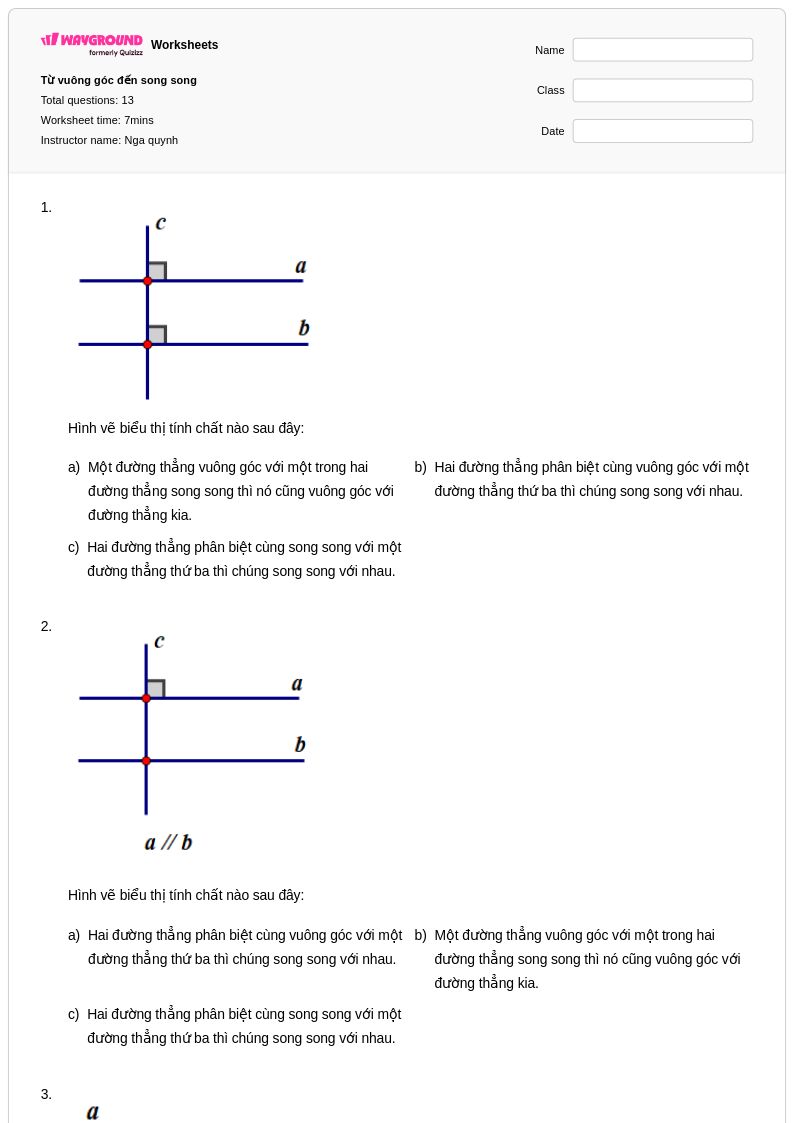
13 Hỏi
12th

10 Hỏi
12th

10 Hỏi
12th

10 Hỏi
12th

10 Hỏi
12th

10 Hỏi
5th - Uni

10 Hỏi
9th - 12th

6 Hỏi
6th - 12th

10 Hỏi
12th

8 Hỏi
12th
Khám phá các bảng tính chủ đề khác cho lớp 12
Khám phá các trang tính Góc nội tiếp có thể in được cho Lớp 12
Góc nội tiếp là một khái niệm cơ bản trong hình học lớp 12, kết nối các mối quan hệ trên đường tròn với các nguyên tắc đo góc. Bộ sưu tập bài tập về góc nội tiếp toàn diện của Wayground cung cấp cho học sinh thực hành có hệ thống trong việc xác định góc tâm và góc nội tiếp, áp dụng định lý góc nội tiếp và giải các bài toán phức tạp liên quan đến đa giác nội tiếp trong đường tròn. Các tài liệu được cấu trúc cẩn thận này củng cố các kỹ năng tư duy hình học quan trọng thông qua các bài toán thực hành nâng cao, từ việc xác định góc cơ bản đến các ứng dụng nâng cao liên quan đến tứ giác nội tiếp và mối quan hệ giữa các cung. Mỗi bài tập đều bao gồm đáp án chi tiết và lời giải từng bước, với các tài liệu có sẵn dưới dạng bản in miễn phí ở định dạng PDF tiện lợi để hỗ trợ cả việc giảng dạy trên lớp và tự học.
Thư viện tài liệu về góc nội tiếp do giáo viên biên soạn của Wayground được xây dựng dựa trên hàng triệu tài liệu giáo dục được phát triển bởi các nhà giáo dục toán học giàu kinh nghiệm, những người hiểu rõ sự phức tạp của các khái niệm hình học nâng cao. Khả năng tìm kiếm và lọc mạnh mẽ của nền tảng cho phép các nhà giáo dục nhanh chóng tìm thấy các bài tập phù hợp với các tiêu chuẩn chương trình giảng dạy cụ thể và phù hợp với trình độ kỹ năng của học sinh, trong khi các công cụ phân hóa tích hợp cho phép tùy chỉnh liền mạch cho các nhu cầu học tập đa dạng. Giáo viên có thể truy cập các tài liệu này ở cả dạng PDF có thể in và dạng kỹ thuật số tương tác, lý tưởng cho môi trường lớp học truyền thống, bài tập về nhà, các buổi ôn tập chuyên sâu và các hoạt động nâng cao cho học sinh giỏi. Sự linh hoạt trong phương pháp giảng dạy này, kết hợp với đáp án đầy đủ và giải thích chi tiết, giúp các nhà giáo dục cung cấp bài tập thực hành kỹ năng tập trung, xây dựng sự tự tin cho học sinh trong việc giải quyết các mối quan hệ hình học phức tạp liên quan đến hình tròn và hình nội tiếp.
